题目内容
已知二次函数f（x）满足f（x+1）-f（x）=2x+3，且f（0）=2，求f（x）的解析式．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：设f（x）=ax2+bx+c，由f（0）=2得c=2，由f（x+1）-f（x）=2x+3，得2ax+a+b=2x+3，解方程组求出a，b的值，从而求出函数的解析式．
解答：
解：设f（x）=ax2+bx+c，由f（0）=2得c=2，
故f（x）=ax2+bx+2．
因为f（x+1）-f（x）=2x+3，
所以a（x+1）2+b（x+1）+2-（ax2+bx+2）=2x+3．
即2ax+a+b=2x+3，
∴
，解得：a=1，b=2，
∴f（x）=x2+2x+2．
故f（x）=ax2+bx+2．
因为f（x+1）-f（x）=2x+3，
所以a（x+1）2+b（x+1）+2-（ax2+bx+2）=2x+3．
即2ax+a+b=2x+3，
∴
|
∴f（x）=x2+2x+2．
点评：本题考查了函数的解析式的求法，待定系数法是常用的方法之一，本题属于基础题．
练习册系列答案
相关题目
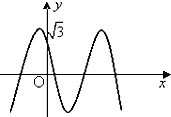如图，函数f（x）=2cos（ωx+θ）（x∈R，ω＞0，0≤θ≤