题目内容
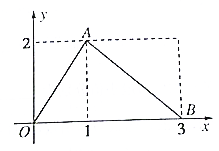 函数y=f(x)的图象是如图所示的折线段OAB,已知点A坐标为(1,2)点B的坐标为(3,0),若P(x,y)是函数g(x)=f(x)(x-1)图象上的动点,则x+y的最大值为( )
函数y=f(x)的图象是如图所示的折线段OAB,已知点A坐标为(1,2)点B的坐标为(3,0),若P(x,y)是函数g(x)=f(x)(x-1)图象上的动点,则x+y的最大值为( )A、
| ||
| B、2 | ||
C、
| ||
| D、4 |
考点:函数解析式的求解及常用方法,函数的最值及其几何意义
专题:函数的性质及应用
分析:根据f(x)的图象,求出f(x)的解析式,从而求出函数y=g(x)的解析式,再求x+y的最大值即可.
解答:
解:根据函数f(x)的图象,得;
当0≤x≤1时,f(x)=2x,
当1<x≤3时,f(x)=-x+3,
∴f(x)=
;
∴函数y=g(x)=f(x)(x-1)
=
,
∴当0≤x≤1时,
x+y=x+2x(x-1)=2x2-x≤1,
当1<x≤3时,
x+y=x+(-x+3)(x-1)=-x2+5x-3≤
;
综上,x+y的最大值为
.
故选:A.
当0≤x≤1时,f(x)=2x,
当1<x≤3时,f(x)=-x+3,
∴f(x)=
|
∴函数y=g(x)=f(x)(x-1)
=
|
∴当0≤x≤1时,
x+y=x+2x(x-1)=2x2-x≤1,
当1<x≤3时,
x+y=x+(-x+3)(x-1)=-x2+5x-3≤
| 13 |
| 4 |
综上,x+y的最大值为
| 13 |
| 4 |
故选:A.
点评:本题考查了根据函数的图象求分段函数解析式的应用问题,也考查了求函数的最值问题,是基础题目.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
已知向量
=(1,n),
=(-1,n),若2
-
与
垂直,则n2的值为( )
| a |
| b |
| a |
| b |
| b |
| A、1 | B、2 | C、3 | D、4 |
已知{an}为等比数列,Sn是它的前n项和.若a2•a3=2a1,且a4与2a7的等差中项为
,则S5=( )
| 5 |
| 4 |
| A、31 | B、32 | C、33 | D、34 |
函数y=sin(
-2x)cos(
+2x)的周期及单调递减区间分别是( )
| π |
| 6 |
| π |
| 6 |
A、
| ||||||||||
B、π(
| ||||||||||
C、
| ||||||||||
D、
|
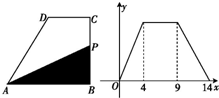 直角梯形ABCD如图,动点P从点B出发,由B→C→D→A沿边运动,设点P运动的路程为x,△ABP的面积为f(x),如果函数y=f(x)的图象如图,则AB的长度为( )
直角梯形ABCD如图,动点P从点B出发,由B→C→D→A沿边运动,设点P运动的路程为x,△ABP的面积为f(x),如果函数y=f(x)的图象如图,则AB的长度为( )