题目内容
已知正三棱锥中，侧面和底面所成的角为
，则侧棱和底面所成角的余弦值为 ．
| π |
| 4 |
考点：直线与平面所成的角
专题：计算题,空间角
分析：设正三棱锥为P-ABC，作正棱锥P-ABC的高PO，作PE垂直于AB，连接OE，则∠PEO为45°，PO=OE，O为底面的中心，CO=AO=BO=2OE，所以AO=2PO，由此能求出该正三棱锥的侧棱与底面所成角的大小．
解答：
解：设正三棱锥为P-ABC，
作正棱锥P-ABC的高PO，作PE垂直于AB，连接OE，则∠PEO为45°，
∴PO=OE，O为底面的中心，
∴CO=AO=BO=2OE，
∴AO=2PO，
∴PA=
PO
∴该正三棱锥的侧棱与底面所成角的余弦值为：
．
故答案为：
．
解：设正三棱锥为P-ABC，作正棱锥P-ABC的高PO，作PE垂直于AB，连接OE，则∠PEO为45°，
∴PO=OE，O为底面的中心，
∴CO=AO=BO=2OE，
∴AO=2PO，
∴PA=
| 5 |
∴该正三棱锥的侧棱与底面所成角的余弦值为：
2
| ||
| 5 |
故答案为：
2
| ||
| 5 |
点评：本题考查二面角的平面角及其求法，解题时要认真审题，注意合理地化立体问题为平面问题．
练习册系列答案
相关题目
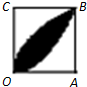在正方形OABC框格内有一块花纹（如图所示），花纹刚好过点O，B，经研究发现花纹边界是函数y=x2与