题目内容
9.设f(x)=alnx+bx2+x在x1=1和x2=2处都取得极值,试求a与b的值,并指出这时f(x)在x1与x2处是取得极大值还是极小值.分析 根据极值的概念,求出a,b值,利用导函数判断函数的单调区间,根据单调区间判断函数的极值.
解答 解:f(x)=alnx+bx2+x,
f'(x)=$\frac{a}{x}$+2bx+1,
∵f'(1)=0,f'(2)=0,
∴a=-$\frac{2}{3}$,b=-$\frac{1}{6}$;
f'(x)=-$\frac{{x}^{2}-3x+2}{3x}$,
当x在(0,1)时,f'(x)<0,f(x)递减,
当x在(1,2)时,f'(x)>0,f(x)递增,
当x在(2,+∞)时,f'(x)<0,f(x)递减,
∴f(x)在x1与处取得极小值,在x2处取得极大值.
点评 考查了函数极值的概念和导函数的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知F1,F2为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,以原点O为圆心,半焦距为半径的圆与椭圆相交于四个点,设位于y轴右侧的两个交点为A,B,若△ABF1为等边三角形,则椭圆的离心率为( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-1 | C. | $\frac{{\sqrt{2}-1}}{2}$ | D. | $\frac{{\sqrt{3}-1}}{3}$ |
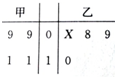 从巍山县庙街镇一所小学的甲、乙两个班级分别随机抽取4名学生的年龄制作出如右所示茎叶图,乙纪录中有一个数据模糊,无法确认,以X表示.
从巍山县庙街镇一所小学的甲、乙两个班级分别随机抽取4名学生的年龄制作出如右所示茎叶图,乙纪录中有一个数据模糊,无法确认,以X表示.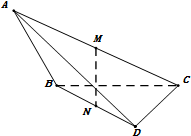 如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.
如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.