题目内容
4.已知过抛物线y2=9x的焦点的弦AB长为12,则直线AB的倾斜角为$\frac{π}{3}$或$\frac{2π}{3}$.分析 首先根据抛物线方程,求得焦点坐标为F( $\frac{9}{4}$,0),从而设所求直线方程为y=k(x-$\frac{9}{4}$).再将所得方程与抛物线y2=9x消去y,利用韦达定理求出x1+x2,最后结合直线过抛物线y2=9x焦点截得弦长为12,得到x1+x2+3=12,求出k,得到直线的倾斜角.
解答 解:∵抛物线方程是y2=9x,
∴2p=9,可得 $\frac{p}{2}$=$\frac{9}{4}$,焦点坐标为F($\frac{9}{4}$,0)
设所求直线方程为y=k(x-$\frac{9}{4}$),
与抛物线y2=9x消去y,得k2x2-($\frac{9}{2}$k2+9)x+$\frac{81}{16}$k2=0
设直线交抛物线与A(x1,y1),B(x2,y2),
由根与系数的关系,得x1+x2=$\frac{\frac{9}{2}{k}^{2}+9}{{k}^{2}}$,
∵直线过抛物线y2=9x焦点,交抛物线得弦长为12,
∴x1+x2+$\frac{9}{2}$=12,可得x1+x2=$\frac{15}{2}$,
因此,$\frac{\frac{9}{2}{k}^{2}+9}{{k}^{2}}$=$\frac{15}{2}$,解之得k2=3,
∴k=tanα=±$\sqrt{3}$,结合α∈[0,π),可得α=$\frac{π}{3}$或$\frac{2π}{3}$.
故答案为:$\frac{π}{3}$或$\frac{2π}{3}$.
点评 本题给出已知方程的抛物线焦点弦长为12,求这条弦所在直线的倾斜角,着重考查了直线倾斜角、抛物线的基本概念和直线与抛物线的位置关系等知识点,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
15.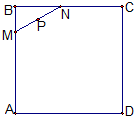 正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )
正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )
 正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )
正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )| A. | $\frac{7}{8}$ | B. | $\frac{π}{16}$ | C. | $1-\frac{π}{16}$ | D. | $\frac{3}{4}+\frac{π}{16}$ |
12.已知点A(1,2,2)、B(1,-3,1),点C在yOz平面上,且点C到点A、B的距离相等,则点C的坐示可以为( )
| A. | (0,1,-1) | B. | (0,-1,6) | C. | (0,1,-6) | D. | (0,1,6) |
19.已知i为虚数单位,复数z=a+bi(a,b∈R)的虚部b记作Im(z),则Im($\frac{-i}{1-i}$)=( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
13.设α,β是第二象限的角,且sinα<sinβ,那么下列不等式成立的是( )
| A. | α<β | B. | cosα<cosβ | C. | tanα<tanβ | D. | sinα>sinβ |
17.设$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$是两个不共线的向量,$\overrightarrow{AB}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$,$\overrightarrow{CB}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{CD}$=3$\overrightarrow{{e}_{1}}$-2k$\overrightarrow{{e}_{2}}$,若A,B,D共线,则k的值为( )
| A. | -$\frac{9}{4}$ | B. | -$\frac{4}{9}$ | C. | -$\frac{3}{8}$ | D. | 不存在 |
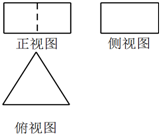 如图为某几何体的三视图,其中俯视图为边长为2的正三角形,正视图为长为2,宽为1的矩形,则该三视图的体积为$\sqrt{3}$,表面积为$6+2\sqrt{3}$.
如图为某几何体的三视图,其中俯视图为边长为2的正三角形,正视图为长为2,宽为1的矩形,则该三视图的体积为$\sqrt{3}$,表面积为$6+2\sqrt{3}$. 现给如图所示的4个区域涂色,要求相邻区域不得使用同一颜色,共有3种颜色可供选择,则不同的 涂色方法共有6种.
现给如图所示的4个区域涂色,要求相邻区域不得使用同一颜色,共有3种颜色可供选择,则不同的 涂色方法共有6种.