题目内容
14.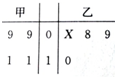 从巍山县庙街镇一所小学的甲、乙两个班级分别随机抽取4名学生的年龄制作出如右所示茎叶图,乙纪录中有一个数据模糊,无法确认,以X表示.
从巍山县庙街镇一所小学的甲、乙两个班级分别随机抽取4名学生的年龄制作出如右所示茎叶图,乙纪录中有一个数据模糊,无法确认,以X表示.(Ⅰ)若这8个学生的平均年龄是9.5岁,求X;
(Ⅱ)有关专家的研究结果显示,儿童身高b(cm)与年龄a(岁)有关系:b=7a+70.在(Ⅰ)的条件下,试分别估计甲、乙两个班级学生的身高;
(Ⅲ)估计哪个班学生的身高更整齐,说明理由.
分析 (Ⅰ)由茎叶图及平均数的定义,代入列方程即可求得X;
(Ⅱ)求得两个班的平均年龄,代入回归直线方程即可估计甲、乙两个班级学生的身高;
(Ⅲ)由茎叶图估计,分别求得甲乙两班学生的身高由(Ⅱ)可知,根据方差公式,求得.D(X)甲,D(X)乙,由D(X)甲>D(X)乙,可知乙班学生的身高更整齐.
解答 解:(Ⅰ)由$\frac{1}{8}(9×2+11×2+X+8+9+10)=9.5$,得X=9;
(Ⅱ)甲班4名同学的平均年龄是a=10岁,
代入公式,得b=140,故估计甲班学生平均身高140cm,
同理,估计乙班学生平均身高是133cm;
(Ⅲ)由(Ⅰ)和(Ⅱ)可知:甲班的四人儿童的身高为:133,133,147,147,
$\overline{{b}_{甲}}$=$\frac{133+133+147+147}{4}$=140,
D(X)甲=$\frac{1}{4}$[(133-140)2+(133-140)2+(147-140)2+(147-140)2]=49,
乙班四人儿童的身高:126,133,133,140,
$\overline{{b}_{乙}}$=$\frac{126+133+133+140}{4}$=133,
D(X)乙=$\frac{1}{4}$[(126-133)2+(133-133)2+(133-133)2+(140-133)2]=24.5,
由D(X)甲>D(X)乙,
∴乙班学生的身高更整齐.
点评 本题考查茎叶图及线性回归方程的应用,考查平均数与方差的应用问题,属于基础题.

练习册系列答案
相关题目
4.已知集合A={x|x2-4=0},B={1,2},则A∩B=( )
| A. | 2 | B. | {-2,2} | C. | {2} | D. | ∅ |
6.如图,ABCD-A1B1C1D1为正方体,则下列结论错误的是( )
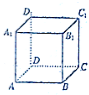

| A. | A1C⊥B1D1 | B. | B1D1∥平面BDC1 | ||
| C. | A1C⊥平面BDC1 | D. | 异面直线AD与BC1所成的角为30° |
 棱长为1的正方形ABCD-A1B1C1D1中,给出以下结论:
棱长为1的正方形ABCD-A1B1C1D1中,给出以下结论: