题目内容
17.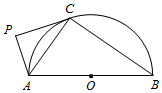 如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足.
如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足.求证:(1)∠PAC=∠CAB;
(2)AC2 =AP•AB.
分析 (1)利用弦切角定理可得:∠ACP=∠ABC.利用圆的性质可得∠ACB=90°.再利用三角形内角和定理即可证明.
(2)由(1)可得:△APC∽△ACB,即可证明.
解答 证明:(1)∵直线PC切半圆O于点C,∴∠ACP=∠ABC.
∵AB为半圆O的直径,∴∠ACB=90°.
∵AP⊥PC,∴∠APC=90°.
∴∠PAC=90°-∠ACP,∠CAB=90°-∠ABC,
∴∠PAC=∠CAB.
(2)由(1)可得:△APC∽△ACB,
∴$\frac{AC}{AB}$=$\frac{AP}{AC}$.
∴AC2 =AP•AB.
点评 本题考查了弦切角定理、圆的性质、三角形内角和定理、三角形相似的判定与性质定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
7.若集合A={x|y=${x^{\frac{1}{2}}$},B={x|y=ln(x+1)},则A∩B=( )
| A. | [0,+∞) | B. | (0,1) | C. | (-1,+∞) | D. | (-∞,-1) |
2.函数f(x)在(-∞,+∞)单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是( )
| A. | [-2,2] | B. | [-1,1] | C. | [0,4] | D. | [1,3] |
6.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
| A. | π | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |