题目内容
12.已知向量$\overrightarrow{a}$=(cosx,sinx),$\overrightarrow{b}$=(3,-$\sqrt{3}$),x∈[0,π].(1)若$\overrightarrow{a}$∥$\overrightarrow{b}$,求x的值;
(2)记f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$,求f(x)的最大值和最小值以及对应的x的值.
分析 (1)根据向量的平行即可得到tanx=-$\frac{\sqrt{3}}{3}$,问题得以解决,
(2)根据向量的数量积和两角和余弦公式和余弦函数的性质即可求出
解答 解:(1)∵$\overrightarrow{a}$=(cosx,sinx),$\overrightarrow{b}$=(3,-$\sqrt{3}$),$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴-$\sqrt{3}$cosx=3sinx,
∴tanx=-$\frac{\sqrt{3}}{3}$,
∵x∈[0,π],
∴x=$\frac{5π}{6}$,
(2)f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$=3cosx-$\sqrt{3}$sinx=2$\sqrt{3}$($\frac{\sqrt{3}}{2}$cosx-$\frac{1}{2}$sinx)=2$\sqrt{3}$cos(x+$\frac{π}{6}$),
∵x∈[0,π],
∴x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
∴-1≤cos(x+$\frac{π}{6}$)≤$\frac{\sqrt{3}}{2}$,
当x=0时,f(x)有最大值,最大值3,
当x=$\frac{5π}{6}$时,f(x)有最小值,最小值-2$\sqrt{3}$.
点评 本题考查了向量的平行和向量的数量积以及三角函数的化简和三角函数的性质,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知复数$z=\frac{{a+{i}}}{{1+{i}}}$(a∈R)的实部为2,则$\overline z$=( )
| A. | 2+i | B. | 2-i | C. | $2-\frac{1}{2}{i}$ | D. | $2+\frac{1}{2}{i}$ |
3.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1 (a>0,b>0)的一条渐近线方程为y=$\frac{\sqrt{5}}{2}$x,且与椭圆$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{3}$=1有公共焦点,则C的方程为( )
| A. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{10}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 |
4.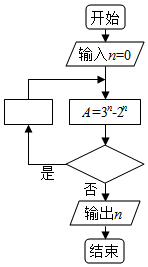 如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在
如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在 和
和 两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( )
 如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在
如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在 和
和 两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( )| A. | A>1000和n=n+1 | B. | A>1000和n=n+2 | C. | A≤1000和n=n+1 | D. | A≤1000和n=n+2 |
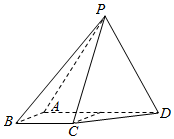 如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°.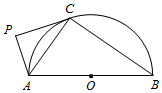 如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足.
如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足.