题目内容
等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=2.设点P,Q满足
=λ
,
=(1-λ)
.若
•
=-10,则λ= .
| AP |
| AB |
| DQ |
| DC |
| BQ |
| CP |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,以BC为x轴,线段BC的中点为坐标原点建立直角坐标系.由于等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=2,可得A(-
,
),B(-
,0),C(
,0),D(
,
).再利用向量的坐标运算和数量积运算即可得出.
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
解答:
解:如图所示,以BC为x轴,线段BC的中点为坐标原点建立直角坐标系.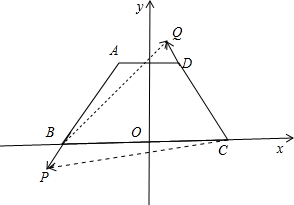
∵等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=2.
∴A(-
,
),B(-
,0),C(
,0),D(
,
).
∵
=λ
,∴
=
+λ(
-
)=(-
-λ,
-
λ).
∵
=(1-λ)
,∴
=
+(1-λ)(
-
)=(
-λ,
λ).
∴
=
-
=(3-λ,
λ),
=
-
=(-2-λ,
-
λ).
∵
•
=-10,
∴(3-λ)(-2-λ)+
λ(
-
λ)=-10,
化为λ2-λ-2=0,
解得λ=2或-1.
故答案为:2或-1.

∵等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=2.
∴A(-
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
∵
| AP |
| AB |
| OP |
| OA |
| OB |
| OA |
| 1 |
| 2 |
| 3 |
| 3 |
∵
| DQ |
| DC |
| OQ |
| OD |
| OC |
| OD |
| 3 |
| 2 |
| 3 |
∴
| BQ |
| OQ |
| OB |
| 3 |
| CP |
| OP |
| OC |
| 3 |
| 3 |
∵
| BQ |
| CP |
∴(3-λ)(-2-λ)+
| 3 |
| 3 |
| 3 |
化为λ2-λ-2=0,
解得λ=2或-1.
故答案为:2或-1.
点评:本题考查了向量的坐标运算和数量积运算,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
已知|
|=1,|
|=
,且(
-
)和
垂直,则
与
的夹角为( )
| a |
| b |
| 2 |
| a |
| b |
| a |
| a |
| b |
| A、60° | B、30° |
| C、45° | D、135° |