题目内容
设函数f(x )=sinxcosx-
cos(π+x)cosx(x∈R)
(1)求f(x)的最小正周期;
(2)若sin(π+α)=
,|α|<
,求f(x)-
的值.
| 3 |
(1)求f(x)的最小正周期;
(2)若sin(π+α)=
| 4 |
| 5 |
| π |
| 2 |
| ||
| 2 |
考点:两角和与差的正弦函数,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质
分析:(1)由两角和与差的正弦函数公式化简函数解析式可得f(x)=sin(2x+
)+
,从而可求f(x)的最小正周期;
(2)先求sinα=-
,又|α|<
,即可求得cosα=
,sin2α=-
,cos2α=-
,化简f(α)-
后代入即可求值.
| π |
| 3 |
| ||
| 2 |
(2)先求sinα=-
| 4 |
| 5 |
| π |
| 2 |
| 3 |
| 5 |
| 24 |
| 25 |
| 7 |
| 25 |
| ||
| 2 |
解答:
解:(1)∵f(x)=sinxcosx-
cos(π+x)cosx
=sinxcosx-
cos(π+x)cosx
=sinxcosx+
cos2x
=
×sinxcosx+
×
=sin(2x+
)+
∴f(x)的最小正周期为T=
=π
(2)∵sin(π+α)=
,
∴sinα=-
,
又|α|<
,
∴cosα=
,sin2α=-
,cos2α=-
∴f(α)-
=sin(2α+
)=sin2αcos
+cos2αsin
=
| 3 |
=sinxcosx-
| 3 |
=sinxcosx+
| 3 |
=
| 1 |
| 2 |
| 3 |
| cos2x+1 |
| 2 |
=sin(2x+
| π |
| 3 |
| ||
| 2 |
∴f(x)的最小正周期为T=
| 2π |
| 2 |
(2)∵sin(π+α)=
| 4 |
| 5 |
∴sinα=-
| 4 |
| 5 |
又|α|<
| π |
| 2 |
∴cosα=
| 3 |
| 5 |
| 24 |
| 25 |
| 7 |
| 25 |
∴f(α)-
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
-24-7
| ||
| 50 |
点评:本题主要考查了两角和与差的正弦函数公式的应用,三角函数的周期性及其求法,属于基础题.

练习册系列答案
相关题目
若把直线l向右平移2个单位,再向下平移1个单位,所得直线与直线l重合,则( )
A、直线l的斜率为-
| ||
| B、直线l的纵截距为1 | ||
| C、直线l的斜率为2 | ||
| D、直线l的纵截距为2 |
某空间几何体的三视图如图所示,则该几何体的表面积是( )
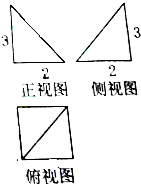

A、10+2
| ||||
B、10+2
| ||||
C、10+
| ||||
D、4+4
|
设函数f(x)=
,在区间[-
,
]上单调递增,则实数a的取值范围为( )
|
| π |
| 2 |
| π |
| 2 |
| A、1<a<2 | ||
B、
| ||
C、1<a≤
| ||
D、
|
函数f(x)=sin(2x+
)的最小正周期为( )
| π |
| 3 |
| A、2π | ||
| B、π | ||
C、
| ||
D、
|
设i为虚数单位,则复数z=1-i的模|z|=( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
已知函数f(x)=-x2-2x,g(x)=
若方程g[f(x)]-a=0的实数根的个数有4个,则a的取值范围( )
|
A、[1,
| ||
| B、[1,+∞) | ||
| C、(1,+∞) | ||
D、(-
|