题目内容
若把直线l向右平移2个单位,再向下平移1个单位,所得直线与直线l重合,则( )
A、直线l的斜率为-
| ||
| B、直线l的纵截距为1 | ||
| C、直线l的斜率为2 | ||
| D、直线l的纵截距为2 |
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:设直线l为y=mx+n,由题意得到mx+n=m(x-2)+n-1,解得m的值即可
解答:
解:设直线l为y=mx+n
∵直线l向右平移2个单位,再向下平移1个单位,所得直线与直线l重合,
∴mx+n=m(x-2)+n-1=mx-2m+n-1,
∴-2m+n+1=n,
∴m=-
∴直线l的斜率为-
,
故选:A
∵直线l向右平移2个单位,再向下平移1个单位,所得直线与直线l重合,
∴mx+n=m(x-2)+n-1=mx-2m+n-1,
∴-2m+n+1=n,
∴m=-
| 1 |
| 2 |
∴直线l的斜率为-
| 1 |
| 2 |
故选:A
点评:本题考查了一次函数的图象和性质,属于基础题

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
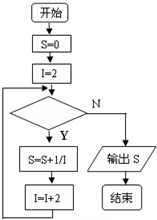
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框内应填入的条件是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |

| A、i≤100 | B、i>100 |
| C、i>50 | D、i≤50 |
已知直线l:y=3x-2的纵截距是( )
| A、-3 | B、-2 | C、3 | D、2 |
当a=3时,下面的程序段输出的y是( )


| A、9 | B、3 | C、10 | D、6 |
已知各项均为正数的等比数列{an}中,3a1,
a3,2a2成等差数列
=( )
| 1 |
| 2 |
| a11-a13 |
| a8-a10 |
| A、27 | B、1 |
| C、-1 | D、-1或27 |