题目内容
13.(x2-x+2y)7的展开式中,x4y4的系数为1680.分析 只有当其中四个因式取2y,一个因式取x2,其余的2个因式都取-x 时,才能可得到含x4y4的项,由此得出结论.
解答 解:∵(x2 -x+2y)7表示7个因式(x2-x+2y)的乘积,当只有4个因式取2y,一个因式取x2,
其余的2个因式都取-x,即可得到含x4y4的项.
故x4y4 的系数为${C}_{7}^{4}$•24•${C}_{3}^{1}$•${C}_{2}^{2}$•(-1)2=1680,
故答案为:1680.
点评 本题主要考查排列组合、二项式定理的应用,乘方的意义,属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
3.将4位老师分配到3个学校去任教,共有分配方案( )
| A. | 81种 | B. | 12种 | C. | 7种 | D. | 256种 |
5.数列{an}的通项an=n2cos$\frac{2nπ}{3}$,其前n项和为Sn,则S60为( )
| A. | 1840 | B. | 1860 | C. | 1880 | D. | 2010 |
5.若某四面体的三视图是全等的等腰直角三角形,且其直角边的长为6,则该四面体的体积是( )
| A. | 108 | B. | 72 | C. | 36 | D. | 9 |
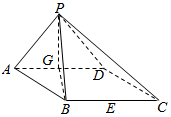 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点,E为BC所在直线上的一点
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点,E为BC所在直线上的一点