题目内容
1.已知数列{an}满足a1=$\frac{1}{2}$,an+1an=2an+1-1,令bn=an-1.(1)求证:数列{$\frac{1}{{b}_{n}}$}为等差数列;
(2)设cn=$\frac{{a}_{n+1}}{{a}_{n}}$,求证:数列{cn}的前n项和Tn<n+$\frac{3}{4}$.
分析 (1)由an+1an=2an+1-1化简可得(an+1-1)(an-1)=(an+1-1)-(an-1),从而可得$\frac{1}{{b}_{n+1}}$-$\frac{1}{{b}_{n}}$=-1,从而证明;
(2)由(1)可求得an=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$,从而可得cn=1+$\frac{1}{n(n+2)}$=1+$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),从而利用裂项求和法求得.
解答 证明:(1)∵an+1an=2an+1-1,
∴(an+1-1)(an-1)=an+1an-an+1-an+1
=2an+1-1-an+1-an+1=(an+1-1)-(an-1),
易知an-1≠0,
即bn+1bn=bn+1-bn,
故$\frac{1}{{b}_{n+1}}$-$\frac{1}{{b}_{n}}$=-1,
又∵$\frac{1}{{b}_{1}}$=$\frac{1}{{a}_{1}-1}$=-2,
∴数列{$\frac{1}{{b}_{n}}$}是以-2为首项,-1为公差的等差数列;
(2)由(1)知,$\frac{1}{{b}_{n}}$=-n-1,故bn=-1=-$\frac{1}{n+1}$,
故an=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$,
故cn=$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{\frac{n+1}{n+2}}{\frac{n}{n+1}}$=1+$\frac{1}{n(n+2)}$=1+$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
故Tn=1+$\frac{1}{2}$(1-$\frac{1}{3}$)+1+$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$)+1+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+…+1+$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$)
=n+$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)
=n+$\frac{3}{4}$-$\frac{1}{2}$($\frac{1}{n+1}$+$\frac{1}{n+2}$)<n+$\frac{3}{4}$.
点评 本题考查了数列的性质的判断与应用,同时考查了构造法与转化思想的应用,属于中档题.

| A. | 125 | B. | 15 | C. | 100 | D. | 10 |
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
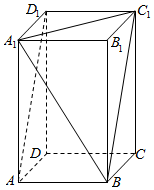 在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=1,AA1=$\sqrt{3}$
在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=1,AA1=$\sqrt{3}$