题目内容
4.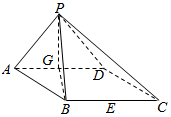 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点,E为BC所在直线上的一点
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点,E为BC所在直线上的一点(1)求证:平面PAD⊥平面PGB;
(2)记$\overrightarrow{BE}$=λ$\overrightarrow{BC}$,当平面PDC和平面PGE所成的二面角的余弦值为$\frac{\sqrt{5}}{5}$时,求λ的值.
分析 (1)连结BD,由正三角形性质的BG⊥AD,由此能证明BG⊥平面PAD,即可证明平面PAD⊥平面PGB;
(2)以G为原点,建立空间直角坐标系G-xyz,由此能利用平面PDC和平面PGE所成的二面角的余弦值为$\frac{\sqrt{5}}{5}$时,求λ的值.
解答 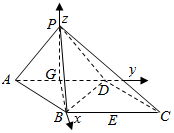 (1)证明:连结BD.
(1)证明:连结BD.
∵ABCD为菱形,且∠DAB=60°
∴△ABD为正三角形.
又G为AD的中点,
∴BG⊥AD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD.
∵BD?平面PGB,
∴平面PAD⊥平面PGB;
(2)解:∵△PAD为正三角形,G为AD的中点,∴PG⊥AD.
∵PG?平面PAD,由(1)得:PG⊥GB.
又由(1)知BG⊥AD.∴PG、BG、AD两两垂直.
故以G为原点,建立如图所示空间直角坐标系G-xyz,PG=PDcos30°=$\sqrt{3}$,GB=ABsin60°=$\sqrt{3}$
所以G(0,0,0),D(0,1,0),P(0,0,$\sqrt{3}$),C($\sqrt{3}$,2,0),E($\sqrt{3}$,2λ,0)
所以$\overrightarrow{PD}$=(0,1,-$\sqrt{3}$),$\overrightarrow{PC}$=($\sqrt{3}$,2,-$\sqrt{3}$),
设平面PCD的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{y-\sqrt{3}z=0}\\{\sqrt{3}x+2y-\sqrt{3}z=0}\end{array}\right.$,
令z=1,则x=-1,y=$\sqrt{3}$,所以$\overrightarrow{n}$=(-1,$\sqrt{3}$,1),
设平面PGE的法向量为$\overrightarrow{m}$=(a,b,c),则
因为$\overrightarrow{PG}$=(0,0,-$\sqrt{3}$),$\overrightarrow{GE}$=($\sqrt{3}$,2λ,0),
所以$\left\{\begin{array}{l}{-\sqrt{3}c=0}\\{\sqrt{3}a+2λb=0}\end{array}\right.$,所以取$\overrightarrow{m}$=(2$\sqrt{3}$,-$\frac{3}{λ}$,0)
因为平面PDC和平面PGE所成的二面角的余弦值为$\frac{\sqrt{5}}{5}$,
所以$\frac{|-2\sqrt{3}-\frac{3\sqrt{3}}{λ}|}{\sqrt{5}•\sqrt{12+\frac{9}{{λ}^{2}}}}$=$\frac{\sqrt{5}}{5}$,所以λ=-$\frac{1}{2}$.
点评 本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,考查平面与平面垂直的证明,解题时正确运用向量法是关键.

| A. | -$\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{12}{25}$ | D. | $\frac{24}{25}$ |
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
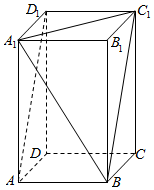 在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=1,AA1=$\sqrt{3}$
在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=1,AA1=$\sqrt{3}$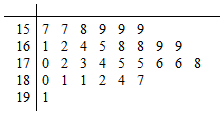 为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”
为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”