题目内容
14．设A（0，1），B（1，3），C（-1，5），D（0，-1），则$\overrightarrow{AB}+\overrightarrow{AC}$等于（ ）| A． | -2$\overrightarrow{AD}$ | B． | 2$\overrightarrow{AD}$ | C． | -3$\overrightarrow{AD}$ | D． | 3$\overrightarrow{AD}$ |
分析 根据向量的坐标运算和向量的共线定理即可求出．
解答 解：∵A（0，1），B（1，3），C（-1，5），D（0，-1），
∴$\overrightarrow{AB}$=（1，2），$\overrightarrow{AC}$=（-1，4），$\overrightarrow{AD}$=（0，-2）
∴$\overrightarrow{AB}+\overrightarrow{AC}$=（0，6）=-3（0，-2）=-3$\overrightarrow{AD}$，
故选：C
点评 本题考查了向量的坐标运算和向量的共线定理，属于基础题．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
2．将函数$y=sin（{ωx+φ}）（{ω＞0，|φ|＜\frac{π}{2}}）$的图象沿x轴向左平移$\frac{π}{3}$个单位长度，得到函数$y=cos（{2x+\frac{π}{4}}）$的图象，则φ=（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{8}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{4}$ |
9．
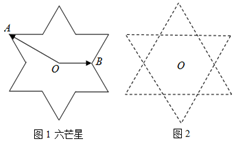如图2，“六芒星”是由两个全等正三角形组成，中心重合于点O且三组对边分别平行．点A，B是“六芒星”（如图1）的两个顶点，动点P在“六芒星”上（内部以及边界），若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$，则x+y的取值范围是（ ）
如图2，“六芒星”是由两个全等正三角形组成，中心重合于点O且三组对边分别平行．点A，B是“六芒星”（如图1）的两个顶点，动点P在“六芒星”上（内部以及边界），若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$，则x+y的取值范围是（ ）| A． | [-4，4] | B． | $[{-\sqrt{21}，\sqrt{21}}]$ | C． | [-5，5] | D． | [-6，6] |
3．设a＞0，b＞0，则“a＞b”是“lna＞lnb”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 既不充分也不必要条件 | D． | 充要条件 |
4．已知数列{an}中，a1=1，an+1=an+n+1，则数列$\{\frac{a_n}{n}\}$的前n项和为（ ）
| A． | $\frac{{{n^2}+5n}}{2}$ | B． | $\frac{{{n^2}+5n}}{4}$ | C． | $\frac{{{n^2}+3n}}{2}$ | D． | $\frac{{{n^2}+3n}}{4}$ |