题目内容
设各项均为正数的数列{an}的前n项和为Sn,且Sn满足Sn2-(n2+n-3)Sn-3(n2+n)=0,n∈N*①
(1)求a1的值;
(2)对①进行因式分解并求数列{an}的通项公式;
(3)证明:对一切正整数n,有
+
+…+
<
②
(1)求a1的值;
(2)对①进行因式分解并求数列{an}的通项公式;
(3)证明:对一切正整数n,有
| 1 |
| a1(a1+1) |
| 1 |
| a2(a2+1) |
| 1 |
| an(an+1) |
| 1 |
| 3 |
考点:数列与不等式的综合
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)直接在数列递推式中取n=1求得a1的值;
(2)由数列递推式因式分解求得Sn,然后由an=Sn-Sn-1(n≥2)求数列{an}的通项公式;
(3)把{an}的通项公式代入
,整理后列项,利用裂项相消法求和后放缩证明数列不等式.
(2)由数列递推式因式分解求得Sn,然后由an=Sn-Sn-1(n≥2)求数列{an}的通项公式;
(3)把{an}的通项公式代入
| 1 |
| an(an+1) |
解答:
(1)解:在Sn2-(n2+n-3)Sn-3(n2+n)=0中,
取n=1,得a12+a1-6=0,
解得:a1=2或a1=-3.
∵数列{an}的各项均为正数,
∴a1=2;
(2)解:由Sn2-(n2+n-3)Sn-3(n2+n)=0,得
(Sn+3)(Sn-n2-n)=0,
即Sn=n2+n.
当n=1时,a1=2.
当n≥2时,an=Sn-Sn-1=n2+n-(n-1)2-(n-1)=2n.
验证n=1时上式成立,
∴an=2n;
(3)证明:由于
=
<
=
(
-
)
故
+
+…+
<
+
(
-
+…+
+
)<
+
=
,
即
+
+…+
<
.
取n=1,得a12+a1-6=0,
解得:a1=2或a1=-3.
∵数列{an}的各项均为正数,
∴a1=2;
(2)解:由Sn2-(n2+n-3)Sn-3(n2+n)=0,得
(Sn+3)(Sn-n2-n)=0,
即Sn=n2+n.
当n=1时,a1=2.
当n≥2时,an=Sn-Sn-1=n2+n-(n-1)2-(n-1)=2n.
验证n=1时上式成立,
∴an=2n;
(3)证明:由于
| 1 |
| an(an+1) |
| 1 |
| 2n(2n+1) |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
故
| 1 |
| a1(a1+1) |
| 1 |
| a2(a2+1) |
| 1 |
| an(an+1) |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 3 |
即
| 1 |
| a1(a1+1) |
| 1 |
| a2(a2+1) |
| 1 |
| an(an+1) |
| 1 |
| 3 |
点评:本题考查了数列递推式,考查了由数列的和求数列的通项公式,训练了裂项相消法求数列的和,考查了放缩法证明数列不等式,是压轴题.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
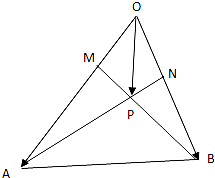 如图,在△OAB中,
如图,在△OAB中,