题目内容
已知函数f（x）=
，试讨论函数f（x）的单调性．
| 2x-1 |
| 2x+1 |
考点：函数单调性的判断与证明
专题：导数的综合应用
分析：求f′（x），根据f′（x）的符号即可判断函数f（x）的单调性．
解答：
解：f′（x）=
=
＞0，函数f（x）的定义域为R；
∴函数f（x）在R上是增函数．
| 2xln2(2x+1)-(2x-1)2xln2 |
| (2x+1)2 |
| 2x+1ln2 |
| (2x+1)2 |
∴函数f（x）在R上是增函数．
点评：考查函数的商的导数的求法，及求函数导数，根据导数符号判断函数单调性的方法．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知
=（2，1），
=（3，-1），则
-
=（ ）
| a |
| b |
| a |
| b |
| A、（5，0） |
| B、（-1，0） |
| C、（-1，2） |
| D、（1，2） |
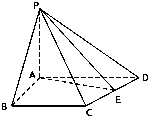在四棱锥P-ABCD中，侧面PAD与侧面PAB都是以A为直角顶点的直角三角形，底面ABCD是直角梯形，AD∥BC，∠ABC=90°，AB=4，BC=3，AD=5，E是CD的中点．