题目内容
已知直线x+y-1=0经过椭圆C:
+
=1(a>b>0)的顶点和焦点F.
(Ⅰ)求此椭圆的标准方程;
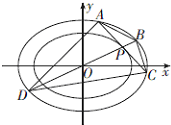
(Ⅱ)斜率为k,且过点F的动直线l与椭圆C交于A,B两点,点A关于x轴的对称点为D,求证直线BD过顶点.
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求此椭圆的标准方程;
(Ⅱ)斜率为k,且过点F的动直线l与椭圆C交于A,B两点,点A关于x轴的对称点为D,求证直线BD过顶点.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)把椭圆短轴上端点坐标及右焦点坐标代入直线x+y-1=0求得b,c的值,进一步求得a的值,则椭圆方程可求;
(Ⅱ)当斜率不为0时设出直线l的方程,和椭圆方程联立得到A,B两点的横纵坐标的和与积,由对称性把D的坐标用A的坐标表示,然后把B,D的坐标代入椭圆方程,通过整体运算把BD的斜率用A,B的坐标表示,写出BD的方程,结合根与系数关系整体代入得到
x+(y2-y1)y=
,由此说明直线BD过定点(2,0),k=0时验证成立.
(Ⅱ)当斜率不为0时设出直线l的方程,和椭圆方程联立得到A,B两点的横纵坐标的和与积,由对称性把D的坐标用A的坐标表示,然后把B,D的坐标代入椭圆方程,通过整体运算把BD的斜率用A,B的坐标表示,写出BD的方程,结合根与系数关系整体代入得到
| 2k2 |
| 1+2k2 |
| 4k2 |
| 1+2k2 |
解答:
(Ⅰ)解:由直线直线x+y-1=0经过椭圆C:
+
=1 (a>b>0)的短轴端点(0,b)和右焦点
F(c,0),可得b=c=1,∴a2=b2+c2=2.
故椭圆C的标准方程为
+y2=1;
(Ⅱ)证明:由椭圆C的方程可得右焦点为F(1,0),
∵直线AB的斜率为k,且直线经过右焦点F,
∴直线AB的方程为y=k(x-1),
设A(x1,y1),B(x2,y2),则点D的坐标为(x1,-y1).
(1)当k≠0时,∵点B,D在椭圆C上,
∴
+
=1,
+(-y1)2=1…①
∴-
+(
-
)=0,依题意知x1≠x2,
∴直线BD的斜率kBD=
=
,
则直线BD的方程为y-y2=
(x-x2)…②
由①②得,
+(y2-y1)y=
-y1y2+1…③
把直线AB的方程代入椭圆C的方程得
+[k(x-1)]2=1,
即(1+2k2)x2-4k2x+2k2-2=0…④
∵x1,x2是方程④的两个实数解,
∴x1+x2=
,x1x2=
…⑤
又y1=k(x1-1),y2=k(x2-1),
∴y1y2=k(x1-1)k(x2-1)=k2[x1x2-(x1+x2)+1]…⑥
把⑤代入⑥得,y1y2=k2[
-
+1]=
…⑦
把⑤⑦代入③得,
•
+(y2-y1)y=
•
-
+1,
即
x+(y2-y1)y=
,
令y=0,解得x=2.
此时,直线BD过定点(2,0);
(2)当k=0时,点A,B为椭圆C的长轴端点,故点D与点A重合,
此时直线BD即为x轴,而x轴过点(2,0),则直线BD也过点(2,0).
综上所述,直线直线BD过定点(2,0).
| x2 |
| a2 |
| y2 |
| b2 |
F(c,0),可得b=c=1,∴a2=b2+c2=2.
故椭圆C的标准方程为
| x2 |
| 2 |
(Ⅱ)证明:由椭圆C的方程可得右焦点为F(1,0),
∵直线AB的斜率为k,且直线经过右焦点F,
∴直线AB的方程为y=k(x-1),
设A(x1,y1),B(x2,y2),则点D的坐标为(x1,-y1).
(1)当k≠0时,∵点B,D在椭圆C上,
∴
| ||
| 2 |
| y | 2 2 |
| ||
| 2 |
∴-
| ||||
| 2 |
| y | 2 1 |
| y | 2 2 |
∴直线BD的斜率kBD=
| y2-(-y1) |
| x2-x1 |
| 1 |
| 2 |
| x1+x2 |
| y1-y2 |
则直线BD的方程为y-y2=
| 1 |
| 2 |
| x1+x2 |
| y1-y2 |
由①②得,
| (x1+x2)x |
| 2 |
| x1x2 |
| 2 |
把直线AB的方程代入椭圆C的方程得
| x2 |
| 2 |
即(1+2k2)x2-4k2x+2k2-2=0…④
∵x1,x2是方程④的两个实数解,
∴x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
又y1=k(x1-1),y2=k(x2-1),
∴y1y2=k(x1-1)k(x2-1)=k2[x1x2-(x1+x2)+1]…⑥
把⑤代入⑥得,y1y2=k2[
| 2k2-2 |
| 1+2k2 |
| 4k2 |
| 1+2k2 |
| -k2 |
| 1+2k2 |
把⑤⑦代入③得,
| 4k2 |
| 1+2k2 |
| x |
| 2 |
| 2k2-2 |
| 1+2k2 |
| 1 |
| 2 |
| -k2 |
| 1+2k2 |
即
| 2k2 |
| 1+2k2 |
| 4k2 |
| 1+2k2 |
令y=0,解得x=2.
此时,直线BD过定点(2,0);
(2)当k=0时,点A,B为椭圆C的长轴端点,故点D与点A重合,
此时直线BD即为x轴,而x轴过点(2,0),则直线BD也过点(2,0).
综上所述,直线直线BD过定点(2,0).
点评:本题考查椭圆方程的求法,考查直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,这是处理这类问题的最为常用的方法,考查了分类讨论的数学思想方法,体现了整体运算思想方法,是高考试卷中的压轴题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 已知曲线C1:
已知曲线C1: