题目内容
设函数f(x)=1-x2,x∈[-
,1].
(1)求f(x)的值域;
(2)求集合M={k|使方程f(x)=k(x+2)有两个不等实根}.
| 2 |
(1)求f(x)的值域;
(2)求集合M={k|使方程f(x)=k(x+2)有两个不等实根}.
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)利用二次函数在x∈[-
,1]的性质即可求得答案.
(2)由题意得x2+kx+2k-1=0在x∈[-
,1]有两个不等实根,根据根的存在条件,列出不等式组,解得即可.
| 2 |
(2)由题意得x2+kx+2k-1=0在x∈[-
| 2 |
解答:
解:(1)∵f(x)=1-x2=-x2+1,
∴其对称轴x=0穿过闭区间[-
,1].
∴函数在x∈[-
,1]时,f(x)max=f(0)=1,
又f(x)在[-
,0]上递增,在[0,1]递减,
f(-
)=-1,f(1)=0,f(-
)<f(1),
∴函数在x∈[-
,1]时,f(x)min=-1,
∴该函数的值域为[-1,1].
(2)∵f(x)=k(x+2)有两个不等实根,
∴1-x2=k(x+2)有两个不等实根,
即x2+kx+2k-1=0在x∈[-
,1]有两个不等实根.
∴
解得,0≤k≤4-2
,
故集合M=[0,4-2
)
∴其对称轴x=0穿过闭区间[-
| 2 |
∴函数在x∈[-
| 2 |
又f(x)在[-
| 2 |
f(-
| 2 |
| 2 |
∴函数在x∈[-
| 2 |
∴该函数的值域为[-1,1].
(2)∵f(x)=k(x+2)有两个不等实根,
∴1-x2=k(x+2)有两个不等实根,
即x2+kx+2k-1=0在x∈[-
| 2 |
∴
|
解得,0≤k≤4-2
| 2 |
故集合M=[0,4-2
| 2 |
点评:本题考查二次函数的性质,以及根的存在条件,考查分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
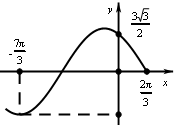 已知ω>0,-π<φ<π,函数f(x)=Asin(ωx+φ)的部分图象如图所示,则f(x)解析式为( )
已知ω>0,-π<φ<π,函数f(x)=Asin(ωx+φ)的部分图象如图所示,则f(x)解析式为( )A、f(x)=3sin(
| ||||
B、f(x)=3sin(
| ||||
C、f(x)=3sin(
| ||||
D、f(x)=3sin(2x+
|
 某英语学习小组共12名同学进行英语听力测试,随机抽取6名同学的测试成绩(单位:分),用茎叶图记录如下,其中茎为十位数,叶为个位数.
某英语学习小组共12名同学进行英语听力测试,随机抽取6名同学的测试成绩(单位:分),用茎叶图记录如下,其中茎为十位数,叶为个位数.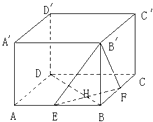 在棱长为a的正方体ABCD-A′B′C′D′中,如图E、F分别为棱AB与BC的中点,EF∩BD=H;
在棱长为a的正方体ABCD-A′B′C′D′中,如图E、F分别为棱AB与BC的中点,EF∩BD=H;