题目内容

下列最大的数是（　　）
A、112（6）
B、41
C、46（9）
D、2B（16）
考点：整除的定义
专题：数系的扩充和复数
分析：首先把每一个选项中的数都化成十进制的数，然后比较大小即可．
解答： 解：112（6）=1×62+1×61+2=44
46（9）=4×91+6=42
28（16）=2×161+8=40
因为44＞42＞41＞40，
所以最大的数是112（6）．
故选：A．
点评：本题主要考查了六进制、九进制、十六进制与十进制的相互转换，属于基础题，解答此题的关键是要熟练地掌握其转化方法．
练习册系列答案
相关题目
对于任意正整数，定义“n的双阶乘n!!”如下：对于n是偶数时，n!!=n•（n-2）•（n-4）…6×4×2；对于n是奇数时，n!!=n•（n-2）•（n-4）…5×3×1．现有如下四个命题：
①（2013!!）•（2014!!）=2014!；
②2014!!=21007•1007!；
③2014!!的个位数是0；
④2015!!的个位数不是5．
正确的命题是
 
．
已知A（-2，-3），B（2，1），C（1，4），D（-7，-4），则有（　　）
A、
AB
与
CD
共线，A，B，C，D四点共线
B、
AB
与
CD
共线，A，B，C，D四点不共线
C、
AB
与
CD
不共线，A，B，C，D四点共线
D、
AB
与
CD
不共线，A，B，C，D四点不共线
给出下列四个命题：
①“三个球全部放入两个盒子，其中必有一个盒子有一个以上的球”是必然事件
②“当x为某一实数时可使x2＜0”是不可能事件
③“明天燕子口要下雪”是必然事件
④“从含有5个次品的100个灯泡中取出5个，5个都是次品”是随机事件．
其中正确命题的个数是（　　）
A、0B、1C、2D、3
二次函数f（x）=ax2+bx+c（x∈R）的部分对应值如下表：
x-3-2-101234
y6M-4-6-6-4n6
可以判断方程ax2+bx+c=0的两个根所在的区间是（　　）
A、（-3，-1）和（2，4）
B、（-3，-1）和（-1，1）
C、（-1，1）和（1，2）
D、（-∞，-3）和（4，+∞）
“x＞0且y＜0”是“xy＜0”的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充要条件
D、既不充分也不必要条件
函数y=2cos2x+6sinx+1的最大值为（　　）
A、10B、9C、8D、7
已知y=f（x）是偶函数，而y=f（x+1）是奇函数，且对任意0≤x≤1，都有f′（x）≥0，则a=f（
98
19
），b=f（
101
17
），c=f（
106
15
）的大小关系是（　　）
A、c＜b＜a
B、c＜a＜b
C、a＜c＜b
D、a＜b＜c
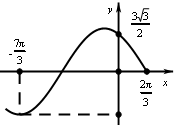已知ω＞0，-π＜φ＜π，函数f（x）=Asin（ωx+φ）的部分图象如图所示，则f（x）解析式为（　　）
A、f（x）=3sin（
1
2
x+
2π
3
）
B、f（x）=3sin（
1
2
x-
π
3
）
C、f（x）=3sin（
1
2
x+
π
3
）
D、f（x）=3sin（2x+
π
3
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网