Question

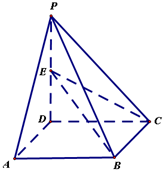如图，四棱锥P-ABCD的底面是正方形，PD⊥面ABCD，E是PD上一点．
（1）求证：AC⊥BE．
（2）若PD=AD=1，且∠PCE的余弦值为

3 10

10

，求三棱锥E-PBC的体积．
（3）在（2）的条件下，求二面角B-AC-E的余弦值．

Answer 1

考点：二面角的平面角及求法,棱柱、棱锥、棱台的体积,直线与平面垂直的性质

专题：空间位置关系与距离,空间角

分析：（1）连接BD，通过证明AC⊥BD，AC⊥PD，利用直线与平面垂直的判定定理证明AC⊥面PBD，然后证明AC⊥BE得证．
（2）PD=AD=1，设PE=x，表示出CE，通过PC=

2

，cos∠PCE=

3

10

，由余弦定理求得：x的值，判断E为PD中点，
转化VE-PBC=

1

2

VP-BCD求解即可．
（3）在（2）的条件下，连结BD交AC于点O，连结OE，说明∠BOE为二面角B-AC-E的平面角．通过解三角形，即可求二面角B-AC-E的余弦值．

解答： 解：（1）连接BD，因为ABCD是正方形，所以AC⊥BD，
又PD⊥面ABCD，得AC⊥PD，
又BD?面PBD，PD?面PBD，BD∩PD=D，所以AC⊥面PBD，
因为BE?面PBD，故AC⊥BE得证；
（2）设PE=x，则CE=

DE2+CD2

=

(1-x)2+1

  
又PC=

2

，cos∠PCE=

3

10

，
∴在△PCE中，由余弦定理x²=CE²+PC²-2CE•PEcoscos∠PCE，
求得：x=

1

2

，即E为PD中点，
所以VE-PBC=

1

2

VP-BCD
V_P-BCD=

1

3

•PD•S_△BCD=

1

3

×1×1×1×

1

2

=

1

6

所以VE-PBC=

1

12

．
（3）连结BD交AC于点O，连结OE，由正方形ABCD可得AC⊥BD，
∵PD⊥面ABCD，AC?ABCD，
∴AC⊥DE，则易得AC⊥OE，
∴∠BOE为二面角B-AC-E的平面角．
由（2）知E为PD中点，则DE=

1

2

，
在正方形ABCD中，OD=

2

2

AD=

2

2

，
∴OE=

DE2+DO2

=

3

2

，
则COS∠DOE=

OD

OE

=

6

3

，
∴COS∠BOE=COS(π-∠DOE)=-COS∠DOE=-

6

3

．

点评：本题考查直线与平面垂直的判定定理以及性质定理的应用，二倍角的平面角的求法，考查转化思想以及计算能力．