题目内容
已知f（
）=x+2
，求f（x）．
| x+1 |
| x |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：设t=
，t≥0，x=t2-1，代入解析式得出f（t）=t2-1+2
，t≥0，就能够得出f（x）解析式．
| x+1 |
| t2-1 |
解答：
解：设t=
，t≥0，x=t2-1，
∵f（
）=x+2
，
∴f（t）=t2-1+2
，t≥0
∴f（x）=x2-1+2
，x≥0，
| x+1 |
∵f（
| x+1 |
| x |
∴f（t）=t2-1+2
| t2-1 |
∴f（x）=x2-1+2
| x2-1 |
点评：本题考查了函数解析式的求解，换元法的运用，容易出错与变量的范围．
练习册系列答案
相关题目
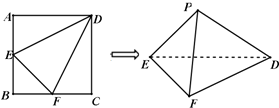如图，在边长为2的正方形ABCD中，E，F分别是AB，BC的中点，将△AED，△BEF，△CFD分别沿DE，EF，DF折起，使A，B，C三点重合于点P．
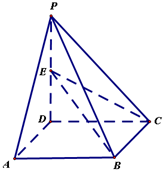如图，四棱锥P-ABCD的底面是正方形，PD⊥面ABCD，E是PD上一点．