题目内容
已知函数y=-3sin（x-
）+2，x∈[0，π]．
（1）求函数的值域以及取得最大值时x的值；
（2）求该函数的单调增区间．
| π |
| 3 |
（1）求函数的值域以及取得最大值时x的值；
（2）求该函数的单调增区间．
考点：正弦函数的单调性,三角函数的最值
专题：计算题,三角函数的图像与性质
分析：（1）由x∈[0，π]可得x-
∈[-
，
]．从而有当x-
=
时，函数y取最小值为-1，当x-
=-
时，即x=0时，函数y取最大值为2+
，
即有函数的值域为[-1，2+
]．
（2）令2kπ+
≤x-
≤2kπ+
，k∈Z可解得：2kπ+
≤x≤2kπ+
，k∈Z，从而得函数的单调增区间为：[2kπ+
，2kπ+
]，k∈Z
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
3
| ||
| 2 |
即有函数的值域为[-1，2+
3
| ||
| 2 |
（2）令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 5π |
| 6 |
| 11π |
| 6 |
| 5π |
| 6 |
| 11π |
| 6 |
解答：
解：（1）∵x∈[0，π]．
∴x-
∈[-
，
]．
∴当x-
=
时，函数y取最小值为-1，
当x-
=-
时，即x=0时，函数y取最大值为2+
，
∴函数的值域为[-1，2+
]．
（2）令2kπ+
≤x-
≤2kπ+
，k∈Z可解得：2kπ+
≤x≤2kπ+
，k∈Z
故函数的单调增区间为：[2kπ+
，2kπ+
]，k∈Z
∴x-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴当x-
| π |
| 3 |
| π |
| 2 |
当x-
| π |
| 3 |
| π |
| 3 |
3
| ||
| 2 |
∴函数的值域为[-1，2+
3
| ||
| 2 |
（2）令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 5π |
| 6 |
| 11π |
| 6 |
故函数的单调增区间为：[2kπ+
| 5π |
| 6 |
| 11π |
| 6 |
点评：本题主要考察了正弦函数的单调性，三角函数的最值的解法，属于基本知识的考查．
练习册系列答案
相关题目
如图是函数y=f（x）=Asin（ωx+φ）（A＞0，ω＞0）图象上的一段，则在区间（0，2π）上，使等式f（x）=f（0）成立的x的集合为
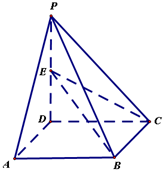如图，四棱锥P-ABCD的底面是正方形，PD⊥面ABCD，E是PD上一点．
如图，在四棱锥中P-ABCD中，底面ABCD为菱形，∠BAD=60°，PA=PD=AD=2，点M在线段PC上，且PM=2MC，N为AD的中点．