题目内容
1.在△ABC中,角A,B,C的对边分别为a,b,c,已知$sinB=\frac{5}{13}$,且a,b,c成等比数列.(Ⅰ)求$\frac{1}{tanA}$+$\frac{1}{tanC}$的值;
(Ⅱ)若accosB=12,求S△ABC及a+c的值.
分析 (Ⅰ)根据正弦定理与等比数列的定义,得出sinAsinC=sin2B;
再利用三角恒等变换计算$\frac{1}{tanA}$+$\frac{1}{tanC}$的值;
(Ⅱ)利用正弦、余弦定理求出三角形的面积和a+c的值.
解答 解:(Ⅰ)△ABC中,$sinB=\frac{5}{13}$,且a,b,c成等比数列,
∴ac=b2,
即sinAsinC=sin2B=$\frac{25}{169}$;
∴$\frac{1}{tanA}$+$\frac{1}{tanC}$=$\frac{cosA}{sinA}$+$\frac{cosC}{sinC}$
=$\frac{sinCcosA+cosCsinA}{sinAsinC}$
=$\frac{sin(A+C)}{sinAsinC}$
=$\frac{sinB}{sinAsinC}$
=$\frac{\frac{5}{13}}{\frac{25}{169}}$
=$\frac{13}{5}$;
(Ⅱ)由accosB=12知cosB>0,
由sinB=$\frac{5}{13}$,得cosB=±$\frac{12}{13}$,(舍去负值)
从而b2=ac=$\frac{12}{cosB}$=13;
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$×13×$\frac{5}{13}$=$\frac{5}{2}$;
由余弦定理,得
b2=(a+c)2-2ac-2accosB,
代入数值,得
13=(a+c)2-2×13×(1+$\frac{12}{13}$),
解得:a+c=3$\sqrt{7}$.
点评 本题考查了三角恒等变换与正弦、余弦定理的应用问题,是综合性题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知过点P(-1,1)且斜率为k的直线l与抛物线y2=x有且只有一个交点,则k的值等于0或$\frac{{-1+\sqrt{2}}}{2}$或$\frac{{-1-\sqrt{2}}}{2}$.
9.已知cos($\frac{π}{2}$+α)=$\frac{3}{5}$,则α∈($\frac{π}{2}$,$\frac{3π}{2}$),则sin2α=( )
| A. | -$\frac{24}{25}$ | B. | -$\frac{16}{25}$ | C. | $\frac{24}{25}$ | D. | $\frac{12}{25}$ |
6.已知变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≤3\\ x+3y≥-k\\ y≤1\end{array}\right.$(k∈Z),且z=2x+y的最大值为6,则k的值为( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
10.已知命题p:x2+x-2>0,命题q:{x|f(x)=lg(2x-3)},则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.函数y=a|sinx|+2(a>0)的单调递增区间是( )
| A. | (-$\frac{π}{2}$,$\frac{π}{2}$) | B. | (-π,-$\frac{π}{2}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{3π}{2}$,2π) |
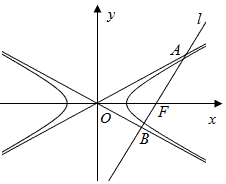 如图所示,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,过F的直线l交双曲线的渐近线于A,B两点,且直线l的倾斜角是渐近线OA倾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,则该双曲线的离心率为$\frac{2\sqrt{3}}{3}$.
如图所示,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,过F的直线l交双曲线的渐近线于A,B两点,且直线l的倾斜角是渐近线OA倾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,则该双曲线的离心率为$\frac{2\sqrt{3}}{3}$.