题目内容
给出下列命题:
①0与{0}表示同一个集合;
②由1,2,3组成的集合可表示为{1,2,3}或{3,2,1};
③方程(x-1)2(x-2)=0的所有解的集合可表示为{1,1,2};
④集合{x|4<x<5}可以用列举法表示;
⑤若全集U={1,2,3}且∁UA={2},则集合A的真子集共有3个.
其中正确命题的序号是 .
①0与{0}表示同一个集合;
②由1,2,3组成的集合可表示为{1,2,3}或{3,2,1};
③方程(x-1)2(x-2)=0的所有解的集合可表示为{1,1,2};
④集合{x|4<x<5}可以用列举法表示;
⑤若全集U={1,2,3}且∁UA={2},则集合A的真子集共有3个.
其中正确命题的序号是
考点:命题的真假判断与应用
专题:集合,简易逻辑
分析:利用元素与集合的关系、集合的性质及其表示法、集合的运算即可判断出.
解答:
解:①0是一个元素(数),而{0}是一个集合,二者是属于与不属于的关系,因此不正确;
②利用集合的无序性可得:由1,2,3组成的集合可表示为{1,2,3}或{3,2,1},正确;
③方程(x-1)2(x-2)=0的所有解的集合可表示为{1,1,2},不正确,因为集合的元素具有互异性,不允许重复,因此方程(x-1)2(x-2)=0的所有解的集合可表示为{1(2),2},其中1(2)表示是二重根,因此不正确;
④集合{x|4<x<5}含有无穷个元素,不能用列举法表示,因此不正确;
⑤若全集U={1,2,3}且∁UA={2},则集合A={1,3},其真子集为∅,{1},{3},共有3个,因此正确.
综上可知:只有②⑤正确.
故答案为:②⑤.
②利用集合的无序性可得:由1,2,3组成的集合可表示为{1,2,3}或{3,2,1},正确;
③方程(x-1)2(x-2)=0的所有解的集合可表示为{1,1,2},不正确,因为集合的元素具有互异性,不允许重复,因此方程(x-1)2(x-2)=0的所有解的集合可表示为{1(2),2},其中1(2)表示是二重根,因此不正确;
④集合{x|4<x<5}含有无穷个元素,不能用列举法表示,因此不正确;
⑤若全集U={1,2,3}且∁UA={2},则集合A={1,3},其真子集为∅,{1},{3},共有3个,因此正确.
综上可知:只有②⑤正确.
故答案为:②⑤.
点评:本题考查了元素与集合的关系、集合的性质及其表示法、集合的运算,属于基础题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
已知函数f(x)=sin(2x+
),则下面说法错误的是( )
| π |
| 3 |
A、f(x)在(0,
| ||
| B、f(x)的最小正周期为π | ||
C、f(x)的图象向右平移
| ||
D、x=-
|
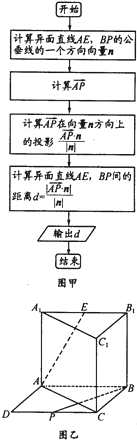 在直三棱柱(侧面垂直于底面的三棱柱)ABC-A1B1C1中,以AB、BC为邻边作平行四边形ABCD,AB⊥BC,AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP,得到如图所示的几何体
在直三棱柱(侧面垂直于底面的三棱柱)ABC-A1B1C1中,以AB、BC为邻边作平行四边形ABCD,AB⊥BC,AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP,得到如图所示的几何体 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题: