题目内容
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
(Ⅰ)试分别估计元件A、元件B为正品的概率;
(Ⅱ)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下:
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下:
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)由题设条件能求出元件A为正品的概率和元件B为正品的概率.
(Ⅱ)(i)设生产的5件元件中正品件数为x,则有次品5-x件,由题意知100x-20(5-x)≥300,由此能求出生产5件元件B所获得的利润不少于300元的概率.
(ii)随机变量X的所有取值为150,90,30,-30,分别求出P(X=150),P(X=90),P(X=30),P(X=-30),由此能求出X的分布列和EX.
(Ⅱ)(i)设生产的5件元件中正品件数为x,则有次品5-x件,由题意知100x-20(5-x)≥300,由此能求出生产5件元件B所获得的利润不少于300元的概率.
(ii)随机变量X的所有取值为150,90,30,-30,分别求出P(X=150),P(X=90),P(X=30),P(X=-30),由此能求出X的分布列和EX.
解答:
(本小题满分12分)
解:(Ⅰ)由题可知元件A为正品的概率为
=
,
元件B为正品的概率为
=
.…(2分)
(Ⅱ)(i)设生产的5件元件中正品件数为x,则有次品5-x件,
由题意知100x-20(5-x)≥300,
得到x=4,5,设“生产5件元件B所获得的利润不少于300元”为事件C,
则P(C)=
(
)4×
+
(
)5=
.…(6分)
(ii)随机变量X的所有取值为150,90,30,-30,
则P(X=150)=
×
=
,
P(X=90)=
×
=
,
P(X=30)=
×
=
,
P(X=-30)=
×
=
,
所以X的分布列为:
…(10分)
EX=150×
+90×
+30×
-30×
=108.…(12分)
解:(Ⅰ)由题可知元件A为正品的概率为
| 40+32+8 |
| 100 |
| 4 |
| 5 |
元件B为正品的概率为
| 40+29+6 |
| 100 |
| 3 |
| 4 |
(Ⅱ)(i)设生产的5件元件中正品件数为x,则有次品5-x件,
由题意知100x-20(5-x)≥300,
得到x=4,5,设“生产5件元件B所获得的利润不少于300元”为事件C,
则P(C)=
| C | 4 5 |
| 3 |
| 4 |
| 1 |
| 4 |
| C | 5 5 |
| 3 |
| 4 |
| 81 |
| 128 |
(ii)随机变量X的所有取值为150,90,30,-30,
则P(X=150)=
| 4 |
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
P(X=90)=
| 1 |
| 5 |
| 3 |
| 4 |
| 3 |
| 20 |
P(X=30)=
| 4 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
P(X=-30)=
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 20 |
所以X的分布列为:
| X | 150 | 90 | 30 | -30 | ||||||||
| P |
|
|
|
|
EX=150×
| 3 |
| 5 |
| 3 |
| 20 |
| 1 |
| 5 |
| 1 |
| 20 |
点评:本题考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知O为坐标原点,P1、P2是双曲线
-
=1上的点.P是线段P1P2的中点,直线OP、P1P2的斜率分别为k1、k2,若2≤k1≤4,则k2的取值范围是( )
| x2 |
| 9 |
| y2 |
| 4 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
集合A={x|1<x<3},B={x|x≤2},则A∩B=( )
| A、{x|x<3} |
| B、{x|2≤x<3} |
| C、{x|1<x≤2} |
| D、{x|1<x<2} |
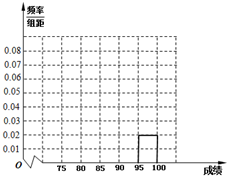 某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.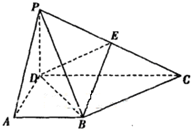 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.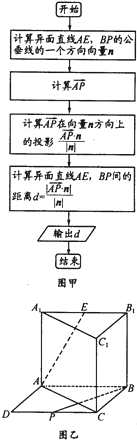 在直三棱柱(侧面垂直于底面的三棱柱)ABC-A1B1C1中,以AB、BC为邻边作平行四边形ABCD,AB⊥BC,AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP,得到如图所示的几何体
在直三棱柱(侧面垂直于底面的三棱柱)ABC-A1B1C1中,以AB、BC为邻边作平行四边形ABCD,AB⊥BC,AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP,得到如图所示的几何体 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题: