题目内容

侧面都是直角三角形的正三棱锥，底面边长为a，则此棱锥的全面积是
 
．
考点：棱柱、棱锥、棱台的侧面积和表面积
专题：空间位置关系与距离
分析：设正三棱锥的侧棱长为b，推出侧棱与底面边长的关系，求出侧棱长，然后求出表面积．
解答： 解：设正三棱锥的侧棱长为b，则由条件知2b2=a2，
∴S表=
3
4
a2+3×
1
2
×
1
2
a2=
3+
3
4
a2．
故答案为：
3+
3
4
a2
点评：本题考查棱锥的表面积，考查计算能力，其中求出棱锥的侧棱长是解答的关键，难度不大是基础题．
练习册系列答案
相关题目
集合A={x|1＜x＜3}，B={x|x≤2}，则A∩B=（　　）
A、{x|x＜3}
B、{x|2≤x＜3}
C、{x|1＜x≤2}
D、{x|1＜x＜2}
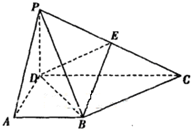在四棱锥P-ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，底面ABCD是直角梯形，AB∥DC，∠ADC=90°，AB=AD=PD=1，CD=2．
（Ⅰ）求证：BC⊥平面PBD：
（Ⅱ）求直线AP与平面PDB所成角的正弦值；
（Ⅲ）设E为侧棱PC上异于端点的一点，
PE
=λ
PC
，试确定λ的值，使得二面角E-BD-P的余弦值为
6
3
．
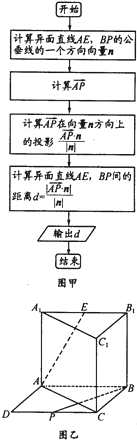在直三棱柱（侧面垂直于底面的三棱柱）ABC-A1B1C1中，以AB、BC为邻边作平行四边形ABCD，AB⊥BC，AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP，得到如图所示的几何体
（1）若AA1=a，图甲给出了异面直线之间的距离的一种算法框图（其中异面直线的公垂线是指两异面直线都垂直且相交的直线）请利用这种方法求异面直线AE和BP之间的距离；
（2）若AA1=2，在线段A1P上是否存在一点F，使得平面AFB⊥平面A1BP？若存在，指出点F的位置，并证明你的结论；若不存在，请说明理由；
（3）若AA1=a，在线段A1C上有一M，过点M做垂直于平面A1ACC1的直线l，与直三棱柱ABC-A1B1C1的其他侧面相交于N，过CM=x，MN=y，求函数y=f（x）的解析式，并据此求出线段MN的长度最大值．
已知函数f(x)=
1
x
+lnx-1，g（x）=（lnx-1）ex+x（其中e为自然对数的底数）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）是否存在实数x0∈（0，+∞），使曲线y=g（x）在点x=x0处的切线与y轴垂直？若存在，求出x0的值；若不存在，请说明理由；
（Ⅲ）若实数m，n满足m＞0，n＞0，求证：nnem≥mnen．
（1）16的四次方根是±2；
（2）集合A={x|y=
x
}，B={y|y=2 x2-1，x∈R}则A∩B=B；
（3）若|log3a|=|log3b|，且a≠b，a＞0，b＞0则ab=1；
（4）若函数f（x+1）是偶函数，则f（x）的图象关于直线x=1对称；
其中正确的序号是
 
$\end{array}$．
如果实数x、y满足
x-y+3≥0
x+y-1≥0
x≤1
，若直线x+ky-1=0将可行域分成面积相等的两部分，则实数k的值为
 
．
已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示，给出关于f（x）的下列命题：
x -1 0 2 4 5
f（x） 1 2 0 2 1
①函数f（x）在[0，1]是减函数，在[1，2]是增函数；
②函数y=f（x）在x=2取到极小值；
③当1＜a＜2时，函数y=f（x）-a有4个零点；
④如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最小值为0．
其中所有正确命题是
 
（写出正确命题的序号）．
在复平面内，复数z满足（3-4i）z=|4+3i|（i为虚数单位），则z的虚部为（　　）
A、-4
B、-
4
5
C、4
D、
4
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网