题目内容
已知f(x)=(1+x)α(1+
)β(x>0),其中α、β为正常数.
(Ⅰ)当α=β=1时,求f(x)的最小值;
(Ⅱ)若y>0,求证:(
)α+β≤(
)α(
)β≤
[(
)α+(
)β]2.
| 1 |
| x |
(Ⅰ)当α=β=1时,求f(x)的最小值;
(Ⅱ)若y>0,求证:(
| α+β |
| x+y |
| α |
| x |
| β |
| y |
| 1 |
| 4 |
| α |
| x |
| β |
| y |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)当α=β=1时,求出f(x)的解析式,利用基本不等式,即可求出函数的最小值;
(Ⅱ)求导数,由导数的正负,可得函数的单调性,从而可得函数的最小值,即可证明结论.
(Ⅱ)求导数,由导数的正负,可得函数的单调性,从而可得函数的最小值,即可证明结论.
解答:
(Ⅰ)解:当α=β=1时,x>0,f(x)=(1+x)(1+
)=x+
+2≥4,
当且仅当x=
即x=1时,等号成立 …(3分)
∴当x=1时,f(x)的最小值为4;
(Ⅱ)证明:∵x>0,其中α、β为正常数,
∴(
)α>0,(
)β>0,
∴
[(
)α+(
)β]2≥
[2
]2=(
)α(
)β…(5分)
又f′(x)=α(1+x)α-1•(1+
)β+(1+x)α•β(1+
)β-1•(-
)…(6分)
=(1+x)α-1•(1+
)β-1•[α(1+
)+(1+x)β(-
)]
=(1+x)α-1•(1+
)β-1•
(αx-β)…(7分)
由x>0,α、β为正常数,得(1+x)α-1•(1+
)β-1•
>0
令f′(x)>0得:x>
,令f′(x)<0得:0<x<
…(8分)
∴f(x)的增函数区间是(
,+∞),减函数区间是(0,
)…(9分)
∴f(x)在x=
处取得最小值,f(x)min=f(
)=(
)α(
)β…(10分)
∴f(
)≤f(
)(x>0,y>0)…(12分)
∴(
)α(
)β≤(
)α(
)β…(13分)
整理得:(
)α+β≤(
)α(
)β…(14分)
∴(
)α+β≤(
)α(
)β≤
[(
)α+(
)β]2.
| 1 |
| x |
| 1 |
| x |
当且仅当x=
| 1 |
| x |
∴当x=1时,f(x)的最小值为4;
(Ⅱ)证明:∵x>0,其中α、β为正常数,
∴(
| α |
| x |
| β |
| y |
∴
| 1 |
| 4 |
| α |
| x |
| β |
| y |
| 1 |
| 4 |
(
|
| α |
| x |
| β |
| y |
又f′(x)=α(1+x)α-1•(1+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
=(1+x)α-1•(1+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
=(1+x)α-1•(1+
| 1 |
| x |
| 1+x |
| x2 |
由x>0,α、β为正常数,得(1+x)α-1•(1+
| 1 |
| x |
| 1+x |
| x2 |
令f′(x)>0得:x>
| β |
| α |
| β |
| α |
∴f(x)的增函数区间是(
| β |
| α |
| β |
| α |
∴f(x)在x=
| β |
| α |
| β |
| α |
| α+β |
| α |
| α+β |
| β |
∴f(
| β |
| α |
| y |
| x |
∴(
| α+β |
| α |
| α+β |
| β |
| x+y |
| x |
| x+y |
| y |
整理得:(
| α+β |
| x+y |
| α |
| x |
| β |
| y |
∴(
| α+β |
| x+y |
| α |
| x |
| β |
| y |
| 1 |
| 4 |
| α |
| x |
| β |
| y |
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,正确求导是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将函数f(x)=
sin2x-cos2x的图象向左平移|m|个单位(m>-
),若所得的图象关于直线x=
对称,则m的最小值为( )
| 3 |
| π |
| 2 |
| π |
| 6 |
A、-
| ||
B、-
| ||
| C、0 | ||
D、
|
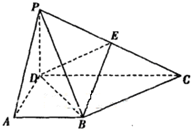 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.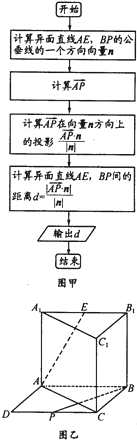 在直三棱柱(侧面垂直于底面的三棱柱)ABC-A1B1C1中,以AB、BC为邻边作平行四边形ABCD,AB⊥BC,AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP,得到如图所示的几何体
在直三棱柱(侧面垂直于底面的三棱柱)ABC-A1B1C1中,以AB、BC为邻边作平行四边形ABCD,AB⊥BC,AB=BC=AA1记线段CD、A1B1的中心分别是P、E连接AE、BP,得到如图所示的几何体