题目内容
(理科)已知椭圆
+
=1(a>b>0)的右焦点F1(2,0),离心率为e.
①若e=
,求椭圆的方程;
②设A、B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,若原点O在以线段MN为直径的圆上,设直线AB斜率为k,若k≥
,求e的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
①若e=
| ||
| 2 |
②设A、B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,若原点O在以线段MN为直径的圆上,设直线AB斜率为k,若k≥
| 3 |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:本题①已知椭圆的焦点,得到参数c的值,再利用椭圆的离心率,得到参数a,b,c的关系,求出a、b的值,得椭圆的方程;②通过几何法得到F1C=CO=
c,可以求出c的值,由方程组
,可得到A点坐标,从而求出OA的斜率,由直线AB斜率为k≥
,求出a的取值范围,从而求出e的取值范围,得到本题结论.
| 1 |
| 2 |
|
| 3 |
解答:
解:①∵椭圆
+
=1(a>b>0)的右焦点F1(2,0),离心率为e=
,
∴
,
∴
.
∴椭圆的方程为
+
=1.
②记线段MN与x轴交点为C.
AF1的中点为M,BF1的中点为N,
∴MN∥AB,F1C=CO=
c.
∵A、B为椭圆上关于原点对称的两点,
∴CM=CN.
∵原点O在以线段MN为直径的圆上,
∴CO=CM=CN=
c.
∴OA=OB=c=2.
∵OA>b,
∴a2=b2+c2<2c2,
∴e=
>
.
设A(x,y),
由
,
得
.
∵直线AB斜率为k≥
,
∴16-8a2+a4≥24a2-3a4,
∴a2≥4+2
,
a≥
+1.
∴e=
≤
-1.
∴离心率e的取值范围为(
,
-1).
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴
|
∴
|
∴椭圆的方程为
| x2 |
| 8 |
| y2 |
| 4 |
②记线段MN与x轴交点为C.
AF1的中点为M,BF1的中点为N,
∴MN∥AB,F1C=CO=
| 1 |
| 2 |
∵A、B为椭圆上关于原点对称的两点,
∴CM=CN.
∵原点O在以线段MN为直径的圆上,
∴CO=CM=CN=
| 1 |
| 2 |
∴OA=OB=c=2.
∵OA>b,
∴a2=b2+c2<2c2,
∴e=
| c |
| a |
| ||
| 2 |
设A(x,y),
由
|
得
|
∵直线AB斜率为k≥
| 3 |
∴16-8a2+a4≥24a2-3a4,
∴a2≥4+2
| 3 |
a≥
| 3 |
∴e=
| c |
| a |
| 3 |
∴离心率e的取值范围为(
| ||
| 2 |
| 3 |
点评:本题考查了函数方程思想,主要上将题中的几何条件代数化,得到相应的等式、不等式、方程,再加以研究.本题有一定的难度,属于中档题.

练习册系列答案
相关题目
若θ为三角形一个内角,且对任意实数x,y=x2cosθ-4xsinθ+6均取正值,则cosθ所在区间为( )
A、(
| ||
B、(0,
| ||
C、(-2,
| ||
D、(-1,
|
函数f(x)=
为R的单调函数,则实数a的取值范围是( )
|
| A、(0,+∞) |
| B、[-1,0) |
| C、(-2,0) |
| D、(-∞,-2) |
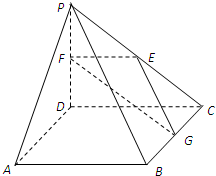 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.