题目内容
已知点（2，3）与抛物线y2=2px（p＞0）的焦点的距离是5，那么p= ．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：先求出抛物线的焦点坐标，再由已知点与抛物线焦点的距离是5，利用两点间距离公式能求出p．
解答：
解：∵抛物线y2=2px（p＞0）的焦点F（
，0），
点（2，3）与抛物线y2=2px（p＞0）的焦点的距离是5，
∴
=5，
解得p=12，或p=-4（舍）．
∴p=12．
故答案为：12．
| p |
| 2 |
点（2，3）与抛物线y2=2px（p＞0）的焦点的距离是5，
∴
(
|
解得p=12，或p=-4（舍）．
∴p=12．
故答案为：12．
点评：本题考查抛物线的参数值的求法，是基础题，解题时要熟练掌握抛物线的简单性质，要注意两点间距离公式的合理运用．
练习册系列答案
初中学业考试导与练系列答案
相关题目
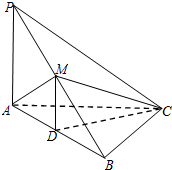如图，在三棱锥P-ABC中，PA⊥AC，PC⊥BC，M为PB的中点，D为AB的中点，且△AMB为正三角形．