题目内容
已知椭圆中心为坐标原点，焦点在x轴上，长半轴长与短半轴长之和为1+
，离心率为
．
（Ⅰ）求椭圆的方程；
（Ⅱ）若C（l，0），过B（-1，0）作直线l交椭圆于M，N两点，且
•
=2，求△MNC的面积．
| 5 |
2
| ||
| 5 |
（Ⅰ）求椭圆的方程；
（Ⅱ）若C（l，0），过B（-1，0）作直线l交椭圆于M，N两点，且
| CM |
| CN |
考点：直线与圆锥曲线的关系,平面向量数量积的运算,椭圆的标准方程
专题：综合题,圆锥曲线的定义、性质与方程
分析：（Ⅰ）设椭圆C：
+
=1（a＞b＞0），根据椭圆长半轴长与短半轴长之和为1+
，离心率为
，建立方程组，求出a，b，即可得出椭圆的方程；
（Ⅱ）分类讨论，设出直线方程，代入椭圆方程，根据
•
=2，利用向量的数量积公式．利用韦达定理求出k，利亚△MNC的面积为
•2|y1-y2|，即可得出结论．
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
2
| ||
| 5 |
（Ⅱ）分类讨论，设出直线方程，代入椭圆方程，根据
| CM |
| CN |
| 1 |
| 2 |
解答：
解：（Ⅰ）设椭圆C：
+
=1（a＞b＞0），则
∵椭圆长半轴长与短半轴长之和为1+
，离心率为
，
∴
，
∴a=
，b=1，
∴椭圆的方程为
+y2=1；
（Ⅱ）设 M（x1，y1）、N （x2，y2），则
直线l斜率不存在时，x=-1代入椭圆方程，可得M（-1，
），N（-1，-
），
∴
•
=（-2，
）•（-2，-
）=4-
≠2；
直线l斜率存在时，设方程为y=k（x+1），代入椭圆方程，消去y并化简整理（1+5k2）x2+10k2x+5k2-5=0，
∴x1+x2=-
，x1x2=
，
∵C（l，0），
∴
•
=（x1-1，y1）•N （x2-1，y2）=（x1-1）（x2-1）+y1y2=（1+k2）x1x2+（k2-1）（x1+x2）+1+k2=2，
∴（1+k2）•
+（k2-1）（-
）+1+k2=2，
∴k=±1，
∴x1+x2=-
=-
，x1x2=
=0，
∴|y1-y2|=|k||x1-x2|=
，
∴△MNC的面积为
•2|y1-y2|=
．
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆长半轴长与短半轴长之和为1+
| 5 |
2
| ||
| 5 |
∴
|
∴a=
| 5 |
∴椭圆的方程为
| x2 |
| 5 |
（Ⅱ）设 M（x1，y1）、N （x2，y2），则
直线l斜率不存在时，x=-1代入椭圆方程，可得M（-1，
2
| ||
| 5 |
2
| ||
| 5 |
∴
| CM |
| CN |
2
| ||
| 5 |
2
| ||
| 5 |
| 4 |
| 5 |
直线l斜率存在时，设方程为y=k（x+1），代入椭圆方程，消去y并化简整理（1+5k2）x2+10k2x+5k2-5=0，
∴x1+x2=-
| 10k2 |
| 1+5k2 |
| 5k2-5 |
| 1+5k2 |
∵C（l，0），
∴
| CM |
| CN |
∴（1+k2）•
| 5k2-5 |
| 1+5k2 |
| 10k2 |
| 1+5k2 |
∴k=±1，
∴x1+x2=-
| 10k2 |
| 1+5k2 |
| 5 |
| 3 |
| 5k2-5 |
| 1+5k2 |
∴|y1-y2|=|k||x1-x2|=
| 5 |
| 3 |
∴△MNC的面积为
| 1 |
| 2 |
| 5 |
| 3 |
点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查向量知识的运用，考查韦达定理，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
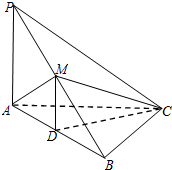如图，在三棱锥P-ABC中，PA⊥AC，PC⊥BC，M为PB的中点，D为AB的中点，且△AMB为正三角形．