��Ŀ����
�����������⣺
�ٺ���y=f��x����ͼ��������[a��b]���������ϣ������ö��ַ�����y=f��x�������䣨a��b���ϵ���㡱��һ����Ҫ�����ǡ�������y=f��x�����䣨a��b��������㡱��
�ں���y=3sin��2x+
����ͼ��ɽ�y=3cos2x��ͼ������ƽ��
����λ���õ���
��ֱ��
-
=1��a��0��b��0����Բx2+y2-2x+4y+3=0�Ļ��ֳ���ȵ������֣���a+b����СֵΪ3+2
��
��������P-ABC�У�PA��PB��PC��ƽ��ABC���ɽ���ȣ����P��ƽ��ABC�ϵ���Ӱ�ǡ�ABC�����ģ�
�ݺ���y=
��ͼ�����ԭ������ĶԳƣ�
������������� ����д������������ı�ţ�
�ٺ���y=f��x����ͼ��������[a��b]���������ϣ������ö��ַ�����y=f��x�������䣨a��b���ϵ���㡱��һ����Ҫ�����ǡ�������y=f��x�����䣨a��b��������㡱��
�ں���y=3sin��2x+
| �� |
| 3 |
| �� |
| 12 |
��ֱ��
| x |
| a |
| y |
| b |
| 2 |
��������P-ABC�У�PA��PB��PC��ƽ��ABC���ɽ���ȣ����P��ƽ��ABC�ϵ���Ӱ�ǡ�ABC�����ģ�
�ݺ���y=
| ||
| |x-3|-3 |
�������������
���㣺���������ж���Ӧ��
ר�⣺������
���������ڢ٣����ö��ַ�����y=f��x�������䣨a��b���ϵ���㣬˵��������y=f��x�����䣨a��b��������㣬��������y=f��x�����䣨a��b��������㣬���������ö��ַ���
���ڢڣ������յ���ʽ������Ϊ���ң�Ȼ�����x�ı仯�жϣ�
���ڢۣ����Բ��Բ�����꣬����ֱ�߷��̣�Ȼ�����û�������ʽ����ֵ��
���ڢܣ��������IJ��⡢��Ӱ���߹��ɵ�ֱ��������ȫ���жϣ�
���ڢݣ��жϺ���Ϊ�溯����
���ڢڣ������յ���ʽ������Ϊ���ң�Ȼ�����x�ı仯�жϣ�
���ڢۣ����Բ��Բ�����꣬����ֱ�߷��̣�Ȼ�����û�������ʽ����ֵ��
���ڢܣ��������IJ��⡢��Ӱ���߹��ɵ�ֱ��������ȫ���жϣ�
���ڢݣ��жϺ���Ϊ�溯����
���
�⣺�ٴ������ö��ַ�����y=f��x�������䣨a��b���ϵ���㣬˵��������y=f��x�����䣨a��b��������㣬��������y=f��x�����䣨a��b��������㣬���������ö��ַ���
�ࡰ������y=f��x�����䣨a��b��������㡱�ǡ��ö��ַ����������䣨a��b����㡱�ı�Ҫ�dz��������
�ڴ���y=3cos2x=3sin2(x+
)����ƽ��
�ɵú���y=3sin(2x+
)��ͼ��
����ȷ����Բ��һ�㷽��x2+y2-2x+4y+3=0֪Բ��Ϊ��1��-2����
��ֱ��
-
=1��Բx2+y2-2x+4y+3=0�Ļ��ֳ���ȵ������֣�
��ֱ��
-
=1���㣨1��-2������
+
=1��
�Ӷ�a+b=(a+b)•(
+
)=3+
+
��3+2
=3+2
�����ҽ���
=
ʱ���Ⱥų�����
��a+b��3+2
��
�ܴ��������IJ��⡢��Ӱ���߹��ɵ�ֱ��������ȫ�ȣ���ӰΪ���ģ�
����ȷ������y=
�Ķ�����Ϊ[-2��0���ȣ�0��2]����ԭ��Գƣ�
��y=
=
=-
Ϊ�溯�����Ӷ�������ͼ�����ԭ������ĶԳƣ�
���������Ǣۢݣ�
�ʴ�Ϊ���ۢݣ�
�ࡰ������y=f��x�����䣨a��b��������㡱�ǡ��ö��ַ����������䣨a��b����㡱�ı�Ҫ�dz��������
�ڴ���y=3cos2x=3sin2(x+
| �� |
| 4 |
| �� |
| 12 |
| �� |
| 3 |
����ȷ����Բ��һ�㷽��x2+y2-2x+4y+3=0֪Բ��Ϊ��1��-2����
��ֱ��
| x |
| a |
| y |
| b |
��ֱ��
| x |
| a |
| y |
| b |
| 1 |
| a |
| 2 |
| b |
�Ӷ�a+b=(a+b)•(
| 1 |
| a |
| 2 |
| b |
| b |
| a |
| 2a |
| b |
|
| 2 |
| b |
| a |
| 2a |
| b |
��a+b��3+2
| 2 |
�ܴ��������IJ��⡢��Ӱ���߹��ɵ�ֱ��������ȫ�ȣ���ӰΪ���ģ�
����ȷ������y=
| ||
| |x-3|-3 |
��y=
| ||
| |x-3|-3 |
| ||
| (3-x)-3 |
| ||
| x |
���������Ǣۢݣ�
�ʴ�Ϊ���ۢݣ�
���������⿼�������������ж���Ӧ�ã����������Ǻ�����ͼ��ƽ�ƣ�ѵ���˺�����ż�Ե��ж�������ѵ�������û�������ʽ����ֵ�����е��⣮

��ϰ��ϵ�д�
 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
�����Ŀ
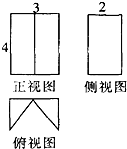 ��ͼ����һ�������������ͼ������ͼ������ͼ��������ͼ������ͼ���Ǿ��Σ���ü�����������
��ͼ����һ�������������ͼ������ͼ������ͼ��������ͼ������ͼ���Ǿ��Σ���ü�����������