题目内容
已知矩阵M=
，记绕原点逆时针旋转
的变换所对应的矩阵为N．
（Ⅰ）求矩阵N；
（Ⅱ）若曲线C：xy=1在矩阵MN对应变换作用下得到曲线C′，求曲线C′的方程．
|
| π |
| 4 |
（Ⅰ）求矩阵N；
（Ⅱ）若曲线C：xy=1在矩阵MN对应变换作用下得到曲线C′，求曲线C′的方程．
考点：几种特殊的矩阵变换
专题：选作题,立体几何
分析：（Ⅰ）利用矩阵变换公式，即可求矩阵N；
（Ⅱ）求出MN，可得坐标之间的关系，代人方程xy=1整理，即可求曲线C′的方程．
（Ⅱ）求出MN，可得坐标之间的关系，代人方程xy=1整理，即可求曲线C′的方程．
解答：
解：（Ⅰ）由已知得，矩阵N=
．…（3分）
（Ⅱ）矩阵MN=
，它所对应的变换为
解得
把它代人方程xy=1整理，得（y′）2-（x′）2=4，
即经过矩阵MN变换后的曲线C′方程为y2-x2=4…（7分）
|
（Ⅱ）矩阵MN=
|
|
|
把它代人方程xy=1整理，得（y′）2-（x′）2=4，
即经过矩阵MN变换后的曲线C′方程为y2-x2=4…（7分）
点评：本题给出矩阵变换，求曲线C在矩阵M对应变换作用下得到的曲线C'方程，着重考查了矩阵与变换的运算、曲线方程的求法等知识，属于中档题．
练习册系列答案
53天天练系列答案
相关题目
直线ax+y+1=0与连接A（2，3），B（-3，2）的线段相交，则a的取值范围是（ ）
| A、[-1，2] |
| B、（-∞，-1]∪[2，+∞） |
| C、[-2，1] |
| D、（-∞，-2]∪[1，+∞） |
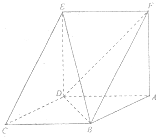如图，已知平行四边形ABCD中，BC=2，BD⊥CD，四边形ADEF为正方形，平面ADEF⊥平面ABCD．
如图为一简单组合体，其底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD=AD=2EC．