题目内容
已知三棱柱ABC-A1B1C1的侧棱与底面边长都等于a,若A1在底面ABC内的射影为△ABC的中心,则AB1与底面ABC所成的角的余弦值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:直线与平面所成的角
专题:空间角
分析:利用题目条件,ED∥A1O,∴ED⊥面ABC,∴作出AB1与底面ABC所成的角∠EAD,在Rt△ADE中,先计算∠EAD正弦值,再求余弦值.
解答:
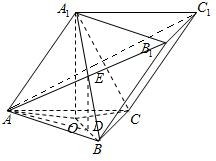 解:设A1在底面ABC内的射影为O,O为△ABC的中心,OA=OB=OC,A1A=A1B=A1C=a,∴正四面体A1-ABC,
解:设A1在底面ABC内的射影为O,O为△ABC的中心,OA=OB=OC,A1A=A1B=A1C=a,∴正四面体A1-ABC,
AB1∩A1B=E,E为A1B中点,D为OB中点,∴ED∥A1O,∴ED⊥面ABC,∴∠EAD即AB1与底面ABC所成的角,OA=OB=
a,在Rt△AA1O中,
A1O=
=
a,ED=
A1O=
a,在正三角形A1AB中,AE=
a,∴在Rt△ADE中,sin∠EAD=
=
,
∴cos∠EAD=
故选:C.
 解:设A1在底面ABC内的射影为O,O为△ABC的中心,OA=OB=OC,A1A=A1B=A1C=a,∴正四面体A1-ABC,
解:设A1在底面ABC内的射影为O,O为△ABC的中心,OA=OB=OC,A1A=A1B=A1C=a,∴正四面体A1-ABC,AB1∩A1B=E,E为A1B中点,D为OB中点,∴ED∥A1O,∴ED⊥面ABC,∴∠EAD即AB1与底面ABC所成的角,OA=OB=
| ||
| 3 |
A1O=
| AA12-OA2 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
| ||
| 2 |
| DE |
| AE |
| ||
| 3 |
∴cos∠EAD=
| ||
| 3 |
故选:C.
点评:本题考查了几何体的结构特征及线面角的定义,考查了转化思想和空间想象能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
下面是关于复数z=
的四个命题:
P1:|z|=2
P2:z2=2i
P3:z的共轭复数为1+i
P4:z的虚部为-1
其中真命题为( )
| 2 |
| -1+i |
P1:|z|=2
P2:z2=2i
P3:z的共轭复数为1+i
P4:z的虚部为-1
其中真命题为( )
| A、P2,P3 |
| B、P1,P2 |
| C、P2,P4 |
| D、P3,P4 |
在极坐标系中,圆ρ=2cosθ+2sinθ的圆心的极坐标是( )
A、(1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、(
|
直线ax+y+1=0与连接A(2,3),B(-3,2)的线段相交,则a的取值范围是( )
| A、[-1,2] |
| B、(-∞,-1]∪[2,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪[1,+∞) |
直线l过点P(1,3),且与x、y轴正半轴围成的三角形的面积等于6的直线方程是( )
| A、3x+y-6=0 |
| B、x+3y-10=0 |
| C、3x-y=0 |
| D、x-3y+8=0 |
 在△ABC中,已知AB=2,AC=2
在△ABC中,已知AB=2,AC=2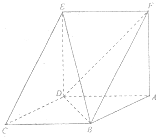 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD.
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD.