题目内容
设s,t是非零实数,
,
是单位向量,当两向量s
+t
,t
-s
的模相等时,
,
的夹角是( )
| i |
| j |
| i |
| j |
| i |
| j |
| i |
| j |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:由题意可得(s
+t
)2=(t
-s
)2,由数量积的定义化简可得cosθ的值,可得答案.
| i |
| j |
| i |
| j |
解答:
解:设
,
的夹角为θ,
由题意可得向量s
+t
,t
-s
的模相等,
∴(s
+t
)2=(t
-s
)2,
化简可得s2+t2+2stcosθ=s2+t2-2stcosθ,
解得cosθ=0,∴θ=
故选:D
| i |
| j |
由题意可得向量s
| i |
| j |
| i |
| j |
∴(s
| i |
| j |
| i |
| j |
化简可得s2+t2+2stcosθ=s2+t2-2stcosθ,
解得cosθ=0,∴θ=
| π |
| 2 |
故选:D
点评:本题考查数量积与向量的夹角,涉及模长公式,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知不重合的两条直线l,m和不重合的两个平面α,β,下列命题正确的是( )
| A、l∥m,l∥β,则m∥β |
| B、α∩β=m,l?α,则l∥β |
| C、α⊥β,l⊥α,则l∥β |
| D、l⊥m,m⊥β,l⊥α,则α⊥β |
下面是关于复数z=
的四个命题:
P1:|z|=2
P2:z2=2i
P3:z的共轭复数为1+i
P4:z的虚部为-1
其中真命题为( )
| 2 |
| -1+i |
P1:|z|=2
P2:z2=2i
P3:z的共轭复数为1+i
P4:z的虚部为-1
其中真命题为( )
| A、P2,P3 |
| B、P1,P2 |
| C、P2,P4 |
| D、P3,P4 |
采用分层抽样的方法抽取一个容量为45的样本,高一年级被抽取20人,高三年级被抽取10人,高二年级共有300人,则这个学校共有高中生( )人.
| A、1350 | B、675 |
| C、900 | D、450 |
已知变量x与y之间一组对应数据如表格所示,经计算它们的回归直线方程为
=2.3x+0.8,定义ei=yi-
i为第i组数据的残差,如果要去除残差绝对值最大的那组数据,则应该去除( )
 |
| y |
 |
| y |
| 序号i | 1 | 2 | 3 | 4 |
| xi | 0 | 1 | 2 | 3 |
| yi | 1 | 3 | 5 | 8 |
| A、第1组 | B、第2组 |
| C、第3组 | D、第4组 |
若复数z=(3-4i)i,则z的虚部为( )
| A、3i | B、3 | C、4i | D、4 |
在极坐标系中,圆ρ=2cosθ+2sinθ的圆心的极坐标是( )
A、(1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、(
|
直线ax+y+1=0与连接A(2,3),B(-3,2)的线段相交,则a的取值范围是( )
| A、[-1,2] |
| B、(-∞,-1]∪[2,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪[1,+∞) |
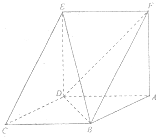 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD.
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD.