题目内容
已知f(x)=|x-1|+|x-a|,
(1)当a=-1时,f(x)≥2的解集;
(2)存在x∈R,f(x)≥2,求a的取值范围.
(1)当a=-1时,f(x)≥2的解集;
(2)存在x∈R,f(x)≥2,求a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)当a=-1时,根据绝对值的意义,-1和1对应点1、-1对应点的距离之和正好等于2,可得f(x)≥2的解集为{x|x≤-1,或 x≥1}.
(2)f(x)表示数轴上的x对应点到1、a对应点的距离之和,它的最小值为|a-1|,由题意可得|a-1|≤2,由此求得a的范围.
(2)f(x)表示数轴上的x对应点到1、a对应点的距离之和,它的最小值为|a-1|,由题意可得|a-1|≤2,由此求得a的范围.
解答:
解:(1)当a=-1时,f(x)≥2,即|x-1|+|x+1|≥2,
而|x-1|+|x-a|表示数轴上的x对应点到1、-1对应点的距离之和,
而-1和1对应点1、-1对应点的距离之和正好等于2,
故f(x)≥2的解集为{x|x≤-1,或 x≥1}.
(2)存在x∈R,f(x)=|x-1|+|x-a|≥2,而f(x)表示数轴上的x对应点到1、a对应点的距离之和,
它的最小值为|a-1|,故|a-1|≤2,求得-1≤a≤3.
而|x-1|+|x-a|表示数轴上的x对应点到1、-1对应点的距离之和,
而-1和1对应点1、-1对应点的距离之和正好等于2,
故f(x)≥2的解集为{x|x≤-1,或 x≥1}.
(2)存在x∈R,f(x)=|x-1|+|x-a|≥2,而f(x)表示数轴上的x对应点到1、a对应点的距离之和,
它的最小值为|a-1|,故|a-1|≤2,求得-1≤a≤3.
点评:本题主要考查绝对值的意义,绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,属于基础题

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
平面内,“动点P到两个定点的距离之和为正常数”是“动点P的轨迹是椭圆”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
某中学共有1000名学生,其中高一年级400人,该校为了了角本校学生近视情况及其形成原因,用分层抽样的方法从该校学生中抽出一个容量为100的样本进行调查,则应从高一年级抽取的人数为( )
| A、10 | B、12 | C、20 | D、40 |
已知集合A={1,2},B={3},则A∪B=( )
| A、{1,2,3} | B、{1,2] |
| C、{3} | D、∅ |
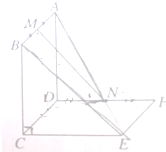 如图,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
如图,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.