题目内容
已知二面角α-l-β大小为60°，点M、N分别在α、β面内，点P到α、β的距离分别为2和3，则△PMN周长的最小值等于 ．
考点：与二面角有关的立体几何综合题
专题：空间位置关系与距离
分析：作出P关于两个平面α，β对称点A、B，连接AB，线段AB与两个平面的交点坐标分别为C，D，连接AP，BP，由已知条件推导出△PMN周长L=PM+PN+MN=AM+MN+BN=AB，由两点之间线段最短可以得出AB即为△PMN周长的最小值．
解答：
解：如图，作出P关于两个平面α，β对称点A、B，连接AB，
线段AB与两个平面的交点坐标分别为C，D，连接AP，BP，
∴四边形CDNM是矩形，
∴MN=CD，
则△PMN周长L=PM+PN+MN=AM+MN+BN=AB，
由两点之间线段最短可以得出AB即为△PMN周长的最小值，
根据题意可知：PM=2，PN=3，
∴AP=4，BP=6，
∵大小为60°的二面角α-a-β，
∴∠MON=60°，
∴∠APB=120°，
根据余弦定理有：
AB2=AP2+BP2-2AP•BP•cos∠APB=42+62-2×4×6×（-1/2）=76，
∴AB=2
，
∴△PMN周长的最小值等于2
．
故答案为：2
．
线段AB与两个平面的交点坐标分别为C，D，连接AP，BP，
∴四边形CDNM是矩形，
∴MN=CD，
则△PMN周长L=PM+PN+MN=AM+MN+BN=AB，
由两点之间线段最短可以得出AB即为△PMN周长的最小值，
根据题意可知：PM=2，PN=3，
∴AP=4，BP=6，
∵大小为60°的二面角α-a-β，
∴∠MON=60°，
∴∠APB=120°，
根据余弦定理有：
AB2=AP2+BP2-2AP•BP•cos∠APB=42+62-2×4×6×（-1/2）=76，
∴AB=2
| 19 |
∴△PMN周长的最小值等于2
| 19 |
故答案为：2
| 19 |
点评：本题考查三角形周长的最小值的求法，是中档题，解题时要认真审题，注意余弦定理的合理运用．
练习册系列答案
一本好题口算题卡系列答案
相关题目
如图，三行三列的方阵中有9个数aij（i=1，2，3；j=1，2，3），从中任取三个数，则这三个数位于不同行不同列的概率是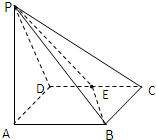
如图，四棱锥P-ABCD中，ABCD为菱形，PA⊥平面ABCD，∠BCD=60°，BC=1，E为CD的中点，PC与平面ABCD成角60°