题目内容
已知集合A={x∈N|
≥1},B={x∈N|log2(x+1)≤1},S⊆A,S∩B≠∅,则集合S的个数为 .
| 3 |
| x |
考点:集合的包含关系判断及应用
专题:集合
分析:依题意,可求得A={1,2,3},B={0,1},再由S⊆A,S中必有1,即可求得答案.
解答:
解:∵A={x∈N|
≥1}={1,2,3},B={x∈N|log2(x+1)≤1}={0,1},
且S⊆A,S∩B≠∅,
∴S中必有1;
∴集合S的个数为
+
+
=4,
故答案为:4.
| 3 |
| x |
且S⊆A,S∩B≠∅,
∴S中必有1;
∴集合S的个数为
| C | 0 2 |
| C | 1 2 |
| C | 2 2 |
故答案为:4.
点评:本题考查集合的包含关系判断及应用,考查组合数的性质,属于基础题.

练习册系列答案
相关题目
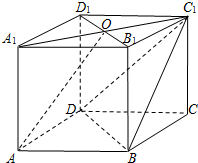 在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1
在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1