题目内容
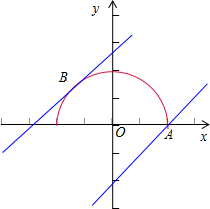
若直线y=x+b与曲线x2+y2=4(y≥0)有公共点,则b的取值范围是 .
考点:直线与圆的位置关系
专题:直线与圆
分析:由题意可得直线y=x+b与半圆x2+y2=4(y≥0)有公共点,当直线过点A(2,0)时,求得 b的值;当直线和半圆相切于点B时,根据圆心到直线的距离等于半径求得b的值,数形结合从而得到b的取值范围.
解答:
 解:由题意可得直线y=x+b与半圆x2+y2=4(y≥0)有公共点,
解:由题意可得直线y=x+b与半圆x2+y2=4(y≥0)有公共点,
如图所示:当直线过点A(2,0)时,可得0=2+b,求得 b=-2.
当直线和半圆相切于点B时,由圆心到直线的距离等于半径可得
=2,求得b=2
,或b=-2
(舍去),
故b的取值范围是[-2,2
],
故答案为:[-2,2
].
 解:由题意可得直线y=x+b与半圆x2+y2=4(y≥0)有公共点,
解:由题意可得直线y=x+b与半圆x2+y2=4(y≥0)有公共点,如图所示:当直线过点A(2,0)时,可得0=2+b,求得 b=-2.
当直线和半圆相切于点B时,由圆心到直线的距离等于半径可得
| |0-0+b| | ||
|
| 2 |
| 2 |
故b的取值范围是[-2,2
| 2 |
故答案为:[-2,2
| 2 |
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
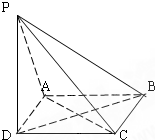 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,PD=AD,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,PD=AD, 一个空间几何体的三视图如图所示,其中主视图和侧视图都是半径为1的圆,且这个几何体是实心球体的一部分,则这个几何体的体积为
一个空间几何体的三视图如图所示,其中主视图和侧视图都是半径为1的圆,且这个几何体是实心球体的一部分,则这个几何体的体积为