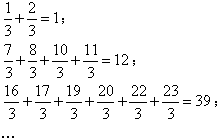题目内容

集合A={x|x是菱形}，集合B={x|x是平行四边形}，则集合A和集合B的关系是
 
，请说明理由
 
．
考点：集合的包含关系判断及应用
专题：集合
分析：根据菱形是四边相等的平行四边形（特殊的平行四边形），可得集合A，B的关系，结合子集的定义可得理由．
解答： 解：由集合A={x|x是菱形}，集合B={x|x是平行四边形}，
∵菱形是四边相等的平行四边形，
但平行四边形不一定是菱形，
故A的元素都属于B，但B中有元素不属于A，
即A是B的真子集，
∴A?B，
故答案为：A?B，菱形是特殊的平行四边形
点评：本题考查的知识点是集合的包含关系判断及应用，其中理解真子集的定义是解答的关键．
练习册系列答案
相关题目
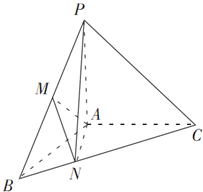如图，在三棱锥P-ABC中，PA⊥面ABC，∠BAC=120°，且AB=AC=AP，M为PB的中点，N在BC上，且AN=
1
3
BC．
（Ⅰ）求证：MN⊥AB；
（Ⅱ）求二面角M-AN-P的余弦值．
已知集合A={x∈N|
3
x
≥1}，B={x∈N|log2（x+1）≤1}，S⊆A，S∩B≠∅，则集合S的个数为
 
．
在极坐标系中，曲线ρ=2sinθ与ρcosθ=-
3
2
的交点的极坐标为
 
（0≤θ＜2π）．
在直角坐标系xOy中，曲线C1的参数方程为
x=2-t
y=2t
（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，曲线C2的极坐标方程为ρ=4cosθ，则C1与C2的两个交点之间的距离等于
 
．
一般地，如果函数y=f（x）的定义域为[a，b]，值域也是[a，b]，则称函数f（x）为“保域函数”，下列函数中是“保域函数”的有
 
．（填上所有正确答案的序号）
①f1（x）=x2-1，x∈[-1，1]；  
②f2（x）=
π
2
sinx，x∈[
π
2
，π]；
③f3（x）=x3-3x，x∈[-2，2]；
④f4（x）=x-lnx，x∈[1，e2]；
⑤f5（x）=
2x
x2-x+1
，x∈[0，2]．
观察下列等式：

则当m＜n且m，n∈N表示最后结果.
3n+1
3
+
3n+2
3
+…+
3m-2
3
+
3m-1
3
=
 
（最后结果用m，n表示最后结果）．
已知f（x-
1
x
）=x2+
1
x2
+1，则f（x）=
 
．
在平行四边形ABCD中E，F分别边BC，CD的中点，且
AE
=
a
，
AF
=
b
，则
BD
=（　　）
A、
1
2
（
b
-
a
）
B、
1
2
（
a
-
b
）
C、2（
a
-
b
）
D、2（
b
-
a
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网