题目内容
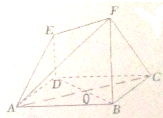 已知如图所示的多面体ABCDEF中,底面ABCD是边长为2的正方形,DE⊥平面ABCD,BF∥DE,且BF=2DE=4.
已知如图所示的多面体ABCDEF中,底面ABCD是边长为2的正方形,DE⊥平面ABCD,BF∥DE,且BF=2DE=4.(1)求多面体ABCDEF的体积;
(2)在棱长FC上是否存在一点P,使EP∥ABCD?
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由于DE⊥平面ABCD,BF∥DE,可得平面BDEF⊥平面ABCD.由于底面ABCD是边长为2的正方形,可得AC⊥BD,梯形BDEF的面积S=
.可得多面体ABCDEF的体积=
×AC×S.
(2)在棱长FC上存在一点P为FC的中点,使EP∥平面ABCD.分别取FC,BC的中点P,Q,连接EP,PQ,DQ.由三角形的中位线定理可得:DE
PQ,因此四边形DEPQ是平行四边形,再利用线面平行的判定定理即可证明.
| (DE+BF)×BD |
| 2 |
| 1 |
| 3 |
(2)在棱长FC上存在一点P为FC的中点,使EP∥平面ABCD.分别取FC,BC的中点P,Q,连接EP,PQ,DQ.由三角形的中位线定理可得:DE
| ∥ |
. |
解答:
解:(1)∵DE⊥平面ABCD,BF∥DE,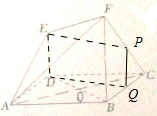
∴平面BDEF⊥平面ABCD.
∵底面ABCD是边长为2的正方形,
∴AC⊥BD,
∴多面体ABCDEF的体积=V四棱锥A-BDEF+V四棱锥C-BDEF.
∵梯形BDEF的面积S=
=
=6
.
∴多面体ABCDEF的体积=
×AC×S=
×2
×6
=8.
(2)分别取FC,BC的中点P,Q,连接EP,PQ,DQ.
由三角形的中位线定理可得:PQ
BF,
又∵DE
BF,
∴DE
PQ,
∴四边形DEPQ是平行四边形,
∴EP∥DQ,
∵EP?平面ABCD,DQ?平面ABCD,
∴EP∥平面ABCD,
因此在棱长FC上存在一点P为FC的中点,使EP∥平面ABCD.

∴平面BDEF⊥平面ABCD.
∵底面ABCD是边长为2的正方形,
∴AC⊥BD,
∴多面体ABCDEF的体积=V四棱锥A-BDEF+V四棱锥C-BDEF.
∵梯形BDEF的面积S=
| (DE+BF)×BD |
| 2 |
(2+4)×2
| ||
| 2 |
| 2 |
∴多面体ABCDEF的体积=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 2 |
(2)分别取FC,BC的中点P,Q,连接EP,PQ,DQ.
由三角形的中位线定理可得:PQ
| ∥ |
. |
| 1 |
| 2 |
又∵DE
| ∥ |
. |
| 1 |
| 2 |
∴DE
| ∥ |
. |
∴四边形DEPQ是平行四边形,
∴EP∥DQ,
∵EP?平面ABCD,DQ?平面ABCD,
∴EP∥平面ABCD,
因此在棱长FC上存在一点P为FC的中点,使EP∥平面ABCD.
点评:本题考查了线面面面平行与垂直的判定与性质定理、三角形的中位线定理、平行四边形的判定与性质定理、四棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
命题p:不等式|
|>
的解集为{x|0<x<1};命题q:“A=B”是“sinA=sinB”成立的必要非充分条件,则( )
| x |
| x-1 |
| x |
| x-1 |
| A、p真q假 |
| B、“p且q”为真 |
| C、“p或q”为假 |
| D、p假q真 |
若(
x+
)n(n∈N*)展开式中含有常数项,则n的最小值是( )
| 3 |
| 1 | |||
|
| A、4 | B、3 | C、12 | D、10 |
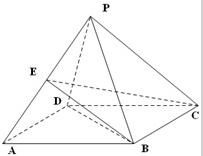 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=