题目内容
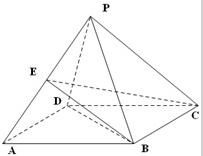 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=| 6 |
(1)求证:PC∥平面EBD.
(2)证明:平面PAC⊥平面PBD.
(3)求三棱锥P-BCE的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)如图所示,连接AC交BD于点O.由底面ABCD是菱形,可得OA=OC,利用三角形的中位线定理可得OE∥PC,再利用线面平行的判定定理即可证明PC∥平面EBD.
(2)底面ABCD是边长为2的菱形,∠BAD=60°,可得△ABD是等边三角形,AO⊥BD,OB=1,OA=
.利用PB=PD=2,OD=OB,可得OP⊥BD.
在Rt△OPB中,利用勾股定理可得OP2=PB2-OB2=22-12=3.可得OP2+OA2=PA2.可得OA⊥OP,OA⊥平面PBD.进而证明平面PAC⊥平面PBD.
(3)由于点E是PA的中点,可得V三棱锥P-BCE=
V三棱锥A-BCP.由于O点是AC的中点,可得V三棱锥A-PBC=2V三棱锥A-POB=2×
×
OP×OB×OA,即可得出.
(2)底面ABCD是边长为2的菱形,∠BAD=60°,可得△ABD是等边三角形,AO⊥BD,OB=1,OA=
| 3 |
在Rt△OPB中,利用勾股定理可得OP2=PB2-OB2=22-12=3.可得OP2+OA2=PA2.可得OA⊥OP,OA⊥平面PBD.进而证明平面PAC⊥平面PBD.
(3)由于点E是PA的中点,可得V三棱锥P-BCE=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
解答:
(1)证明:如图所示,连接AC交BD于点O.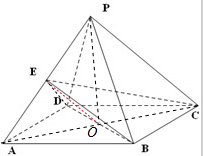
∵底面ABCD是菱形,
∴OA=OC,
又∵E为PA的中点,∴EO∥PC,
而PC?平面BED,EO?平面BED,
∴PC∥平面EBD.
(2)证明:∵底面ABCD是边长为2的菱形,∠BAD=60°,
∴△ABD是等边三角形,AO⊥BD,
∴OB=1,OA=
.
∵PB=PD=2,OD=OB,
∴OP⊥BD.
在Rt△OPB中,OP2=PB2-OB2=22-12=3.
∵PA=
,
∴OP2+OA2=3+3=6=PA2.
∴OA⊥OP.
又OP∩BD=O,
∴OA⊥平面PBD.
∵AO?平面PAC,
∴平面PAC⊥平面PBD.
(3)解:∵点E是PA的中点,
∴V三棱锥P-BCE=
V三棱锥A-BCP.
∵O点是AC的中点,
∴V三棱锥A-PBC=2V三棱锥A-POB=2×
×
OP×OB×OA=
×
×1×
=1.
∴V三棱锥P-BCE=
V三棱锥A-BCP=
.

∵底面ABCD是菱形,
∴OA=OC,
又∵E为PA的中点,∴EO∥PC,
而PC?平面BED,EO?平面BED,
∴PC∥平面EBD.
(2)证明:∵底面ABCD是边长为2的菱形,∠BAD=60°,
∴△ABD是等边三角形,AO⊥BD,
∴OB=1,OA=
| 3 |
∵PB=PD=2,OD=OB,
∴OP⊥BD.
在Rt△OPB中,OP2=PB2-OB2=22-12=3.
∵PA=
| 6 |
∴OP2+OA2=3+3=6=PA2.
∴OA⊥OP.
又OP∩BD=O,
∴OA⊥平面PBD.
∵AO?平面PAC,
∴平面PAC⊥平面PBD.
(3)解:∵点E是PA的中点,
∴V三棱锥P-BCE=
| 1 |
| 2 |
∵O点是AC的中点,
∴V三棱锥A-PBC=2V三棱锥A-POB=2×
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 3 |
∴V三棱锥P-BCE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了菱形的性质、三角形的中位线定理、线面平行的判定定理、线面垂直与面面垂直的判定性质定理、三棱锥的体积计算公式,考查了了推理能力与计算能力,属于难题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
设A={ x||x-2|≤3},B={ x|x<t},若A∩B=φ,则实数t的取值范围是( )
| A、t<-1 | B、t>5 |
| C、t≤-1 | D、t≥5 |
函数y=sinxcos2x在区间[0,
]上的最大值是( )
| π |
| 2 |
| A、0 | ||||
B、
| ||||
C、
| ||||
| D、1 |
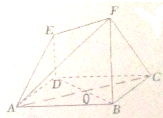 已知如图所示的多面体ABCDEF中,底面ABCD是边长为2的正方形,DE⊥平面ABCD,BF∥DE,且BF=2DE=4.
已知如图所示的多面体ABCDEF中,底面ABCD是边长为2的正方形,DE⊥平面ABCD,BF∥DE,且BF=2DE=4.