题目内容
若（
x+
）n（n∈N*）展开式中含有常数项，则n的最小值是（ ）
| 3 |
| 1 | |||
|
| A、4 | B、3 | C、12 | D、10 |
考点：二项式定理的应用
专题：二项式定理
分析：根据题意，利用二项式展开式的通项公式Tr+1，求出n与r的表达式，结合r，n∈N*，求出n的最小值．
解答：
解：∵（
x+
）n（n∈N*）展开式中含有常数项，
∴Tr+1=
•(
x)n-r•(
)r=
•(
)n-r•xn-
r，
令n-
r=0，
解得r=
n；
又r，n∈N*，
∴n的最小值是4．
故选：A．
| 3 |
| 1 | |||
|
∴Tr+1=
| C | r n |
| 3 |
| 1 | |||
|
| C | r n |
| 3 |
| 4 |
| 3 |
令n-
| 4 |
| 3 |
解得r=
| 3 |
| 4 |
又r，n∈N*，
∴n的最小值是4．
故选：A．
点评：本题考查了二项式定理的应用问题，解题时应利用展开式的通项公式Tr+1进行解答，是基础题．
练习册系列答案
相关题目
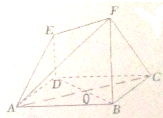已知如图所示的多面体ABCDEF中，底面ABCD是边长为2的正方形，DE⊥平面ABCD，BF∥DE，且BF=2DE=4．