题目内容
命题p：不等式|
|＞
的解集为{x|0＜x＜1}；命题q：“A=B”是“sinA=sinB”成立的必要非充分条件，则（ ）
| x |
| x-1 |
| x |
| x-1 |
| A、p真q假 |
| B、“p且q”为真 |
| C、“p或q”为假 |
| D、p假q真 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：通过解不等式得到p是真命题，结合三角函数的性质得到q是假命题，从而得到答案．
解答：
解：由|
|＞
；可得
＜0，
∴0＜x＜1，故P为真命题
∵sinA=sinB
由正弦定理可得
=
，
∴a=b⇒A=B
即sinA=sinB⇒A=B，是必要条件，
若A=B，则A=B⇒sinA=sinB，是充分条件，
∴A=B”是“sinA=sinB成立的充要条件故q是假命题
故选：A
| x |
| x-1 |
| x |
| x-1 |
| x |
| x-1 |
∴0＜x＜1，故P为真命题
∵sinA=sinB
由正弦定理可得
| a |
| sinA |
| b |
| sinB |
∴a=b⇒A=B
即sinA=sinB⇒A=B，是必要条件，
若A=B，则A=B⇒sinA=sinB，是充分条件，
∴A=B”是“sinA=sinB成立的充要条件故q是假命题
故选：A
点评：本题考查了充分必要条件，考查了不等式的解法以及三角函数问题，本题属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
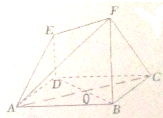已知如图所示的多面体ABCDEF中，底面ABCD是边长为2的正方形，DE⊥平面ABCD，BF∥DE，且BF=2DE=4．