题目内容
若正数m、n满足mn-m-n=3，则点（m，0）到直线x-y+n=0的距离最小值是 ．
考点：点到直线的距离公式
专题：直线与圆
分析：把已知的等式变形，得到（m-1）（n-1）≥4，写出点到直线的距离，然后利用基本不等式得答案．
解答：
解：点（m，0）到直线x-y+n=0的距离为d=
=
|m+n|，
∵mn-m-n=3，
∴（m-1）（n-1）=4，（m-1＞0，n-1＞0），
∴（m-1）+（n-1）≥2
=4，
∴m+n≥6，
则d=
=
|m+n|≥3
．
故答案为：3
．
| |m+n| | ||
|
| ||
| 2 |
∵mn-m-n=3，
∴（m-1）（n-1）=4，（m-1＞0，n-1＞0），
∴（m-1）+（n-1）≥2
| (m-1)(n-1) |
∴m+n≥6，
则d=
| |m+n| | ||
|
| ||
| 2 |
| 2 |
故答案为：3
| 2 |
点评：本题考查了的到直线的距离公式，考查了利用基本不等式求最值，是基础题．
练习册系列答案
相关题目
函数f（x）=ln（3x-2）的定义域是（ ）
| A、[1，+∞） | ||
B、（
| ||
C、[
| ||
D、（
|
设A={ x||x-2|≤3}，B={ x|x＜t}，若A∩B=φ，则实数t的取值范围是（ ）
| A、t＜-1 | B、t＞5 |
| C、t≤-1 | D、t≥5 |
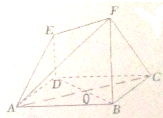已知如图所示的多面体ABCDEF中，底面ABCD是边长为2的正方形，DE⊥平面ABCD，BF∥DE，且BF=2DE=4．