题目内容
已知a＞b＞1，P=
，Q=
（lga+lgb），R=lg
，比较P、Q、R的大小．
| lgalgb |
| 1 |
| 2 |
| a+b |
| 2 |
考点：不等式比较大小
专题：不等式的解法及应用
分析：根据基本不等式
≥
，进行解答即可．
| a+b |
| 2 |
| ab |
解答：
解：∵a＞b＞1，∴lga＞lgb＞0，
∵
＞
，
∴lg（
）＞lg
=
lg（ab）=
（lga+lgb），
∴R＞Q；
又∵
（lga+lgb）＞
，
∴Q＞P；
综上，P＜Q＜R．
∵
| a+b |
| 2 |
| ab |
∴lg（
| a+b |
| 2 |
| ab |
| 1 |
| 2 |
| 1 |
| 2 |
∴R＞Q；
又∵
| 1 |
| 2 |
| lga•lgb |
∴Q＞P；
综上，P＜Q＜R．
点评：本题考查了基本不等式的性质的应用问题，解题时应注意基本不等式的应用条件是什么．
练习册系列答案
相关题目
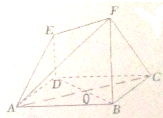已知如图所示的多面体ABCDEF中，底面ABCD是边长为2的正方形，DE⊥平面ABCD，BF∥DE，且BF=2DE=4．