题目内容
我们把正切函数在整个定义域内的图象看作一组“平行曲线”,而“平行曲线”具有性质:任意两条平行直线与两条相邻的“平行曲线”相交,被截得的线段长度相等.已知函数f(x)=tan(ωx+
)(ω>0)图象中的两条相邻“平行曲线”与直线y=2013相交于A,B两点,且|AB|=2,f(
)=( )
| π |
| 3 |
| 1 |
| 2 |
A、2-
| ||||
B、-2-
| ||||
C、
| ||||
D、
|
考点:正切函数的图象
专题:三角函数的图像与性质
分析:首先,根据平行直线与平行曲线截得的线段长度相等,得到|AB|=2,也就是周期为2,然后,利用周期公式,求解ω的值,然后,再求解f(
)的值即可.
| 1 |
| 2 |
解答:
解:∵T=|AB|=2,
∴
=2,
∴ω=
,
∴f(x)=tan(
x+
),
∴f(
)=tan(
+
)
=
=-2-
,
故选:B.
∴
| π |
| ω |
∴ω=
| π |
| 2 |
∴f(x)=tan(
| π |
| 2 |
| π |
| 3 |
∴f(
| 1 |
| 2 |
| π |
| 4 |
| π |
| 3 |
=
1+
| ||
1-
|
=-2-
| 3 |
故选:B.
点评:本题重点考查了正切函数的周期性、两角和的正切公式等知识,属于中档题,本题解题关键是准确理解给定的信息,然后,抽象出该函数的周期为2,这个是突破口.

练习册系列答案
相关题目
函数y=|sinx|(-
<x<
)的大致图象是( )
| π |
| 2 |
| π |
| 2 |
A、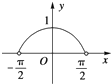 |
B、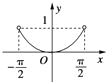 |
C、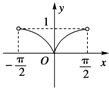 |
D、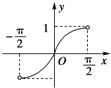 |
6本不同的书分给甲、乙、丙三人,每人两本,不同的分法种数是( )
A、
| ||||||||||
B、
| ||||||||||
C、6A
| ||||||||||
D、C
|
函数f(x)=1-lnx的零点所在的区间是( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
若a>b,c>d且c+d<0,则下列不等式一定成立的是( )
| A、ac>bc |
| B、ac<bc |
| C、ad>bd |
| D、ad<bd |
袋子中有3个红球和2个黑球,从中摸出一个球,该球为黑球的概率是( )
A、
| ||
| B、1 | ||
C、
| ||
D、
|