若复数z满足iz=1+i.则z的共轭复数$\overline{z}$在复平面内所对应点的坐标为( )A．(1.1)B．C．D．题目和参考答案——青夏教育精英家教网—

题目内容

12．若复数z满足iz=1+i，则z的共轭复数$\overline{z}$在复平面内所对应点的坐标为（　　）

A．

（1，1）

B．

（1，-1）

C．

（-1，1）

D．

（-1，-1）

分析利用复数的运算法则、共轭复数的定义、几何意义即可得出．

解答解：iz=1+i，∴-i•iz=-i（1+i），∴z=-i+1．
则z的共轭复数$\overline{z}$=1+i在复平面内所对应点的坐标为（1，1）．
故选：A．

点评本题考查了复数的运算法则、共轭复数的定义、几何意义，考查了推理能力与计算能力，属于基础题．

练习册系列答案

3．设集合A={3，log₂（a-2）}，B={a，a+b}，若A∩B={1}，则b的值为（　　）

20．某学校食堂在高一年级学生中抽查了100名学生进行饮食习惯调查，结果如表：

	喜欢吃辣	不喜欢吃辣	合计
男生	30	10	40
女生	25	35	60
合计	55	45	100

（I）从这100人中随机抽取1人，求抽到喜欢吃辣的学生概率；
（II）试判断有多大把握认为喜欢吃辣与性别有关；
（III）已知在被调查的学生中有5人来自一班，其中有2人喜欢吃辣，从这5人中随机抽取3人，求其中恰有1人喜欢吃辣的概率．
下面临界值表仅供参考：

P（K²≥k₀）	0.15	100．	0.05	0.025	0.010	0.005	0.001
k₀	2.072	2.706	8411．	5.024	6.635	7.879	10.828

$（{参考公式：{K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}，其中n=a+b+c+d}）$．

7．函数f（x）=（cosx）•ln|x|的大致图象是（　　）

	A．			B．
	C．			D．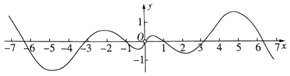

17．函数f（x）是定义在R上的偶函数，其导函数为f′（x），当x＜0时，3f（x）+xf′（x）＜0恒成立，则下列结论正确的是（　　）

	A．	f（1）＜2016f（$\root{3}{2016}$）＜2017f（$\root{3}{2017}$）		B．	2017f（$\root{3}{2017}$）＜f（1）＜2016f（$\root{3}{2016}$）
	C．	2016f（$\root{3}{2016}$）＜f（1）＜2017f（$\root{3}{2017}$）		D．	2017f（$\root{3}{2017}$）＜2016f（$\root{3}{2016}$）＜f（1）

4．设△ABC的内角A，B，C的对边分别为a，b，c，若cosA=$\frac{3}{5}$，sinB=$\frac{{\sqrt{2}}}{2}$，a=8，则c=7$\sqrt{2}$．

20．已知函数f（x）=ax²+（1-2a）x-lnx（a∈R）．
（1）求函数f（x）在区间[1，2]上的最大值；
（2）若A（x₁，y₁），B（x₂，y₂），C（x₀，y₀）是函数f（x）图象上不同的三点，且x₀=$\frac{{{x_1}+{x_2}}}{2}$，试判断f′（x₀）与$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$之间的大小关系，并证明．

试题分类