题目内容
4.已知函数f(x)=(t+1)lnx+tx2+3t,t∈R.(1)若t=0,求证:当x≥0时,f(x+1)≥x-$\frac{1}{2}$x2;
(2)若f(x)≥4x对任意x∈[1,+∞)恒成立,求t的取值范围.
分析 (1)求出函数f(x)的解析式,问题转化为证明ln(x+1)≥x-$\frac{1}{2}$x2;令g(x)=ln(x+1)-x+$\frac{1}{2}$x2,(x≥0);根据函数的单调性证明即可;
(2)问题转化为(t+1)lnx+tx2+3t-4x≥0,令φ(x)=(t+1)lnx+tx2+3t-4x,根据函数的单调性求出t的范围即可.
解答 解:(1)证明:t=0时,f(x)=lnx,f(x+1)=ln(x+1),
即证ln(x+1)≥x-$\frac{1}{2}$x2;
令g(x)=ln(x+1)-x+$\frac{1}{2}$x2,(x≥0);
则g′(x)=$\frac{{x}^{2}}{x+1}$>0,
∴g(x)在(0,+∞)递增,
∴g(x)≥g(0)=0,
即l(x+1)≥x-$\frac{1}{2}$x2;
(2)由f(x)≥4x⇒(t+1)lnx+tx2+3t-4x≥0,
令φ(x)=(t+1)lnx+tx2+3t-4x,
首先由φ(1)≥0⇒t≥1,
此时φ′(x)=$\frac{2{tx}^{2}-4x+t+1}{x}$,
令h(x)=2tx2-4x+t+1,
∵t≥1,∴△=16-8t(t+1)<0,
∴h(x)>0恒成立,
即φ′(x)>0,φ(x)在[1,+∞)递增,
故φ(x)≥φ(1)=4t-4≥0,
综上,t≥1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知向量$\overrightarrow{OM}=(3,-2),\overrightarrow{ON}=(-5,-1),则\overrightarrow{MN}等于$( )
| A. | (8,-1) | B. | (-8,1) | C. | (-2,-3) | D. | (-15,2) |
15.交强险是车主必须为机动车购买的险种.若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
(Ⅰ)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有六辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两辆车中恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
| 交强险浮动因素和浮动费率比率表 | ||
| 浮动因素 | 浮动比率 | |
| A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
| A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
| A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
| 类型 | A1 | A2 | A3 | A4 | A5 | A6 |
| 数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有六辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两辆车中恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
19.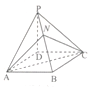 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积之比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积之比为( )
 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积之比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积之比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:6 |
16.下列命题中的真命题为( )
| A. | ?x0∈Z,使得1<4x0<3 | B. | ?x0∈Z,使得5x0+1=0 | ||
| C. | ?x∈R,x2-1=0 | D. | ?x∈R,x2+x+2>0 |
14.执行如图所示的程序框图,那么输出的S为( )


| A. | -2 | B. | $\frac{1}{2}$ | C. | $\frac{4}{3}$ | D. | 3 |
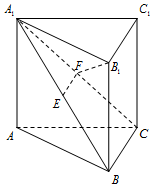 如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点.
如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点.