题目内容
12.已知侧棱与底面垂直的三棱柱ABC-A1B1C1满足AA1=2AB=2BC=4,∠ABC=90°,则其外接球的表面积为24π.分析 根据题意判断直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,我们可以把直三棱柱ABC-A1B1C1补成正四棱柱,则正四棱柱的体对角线是其外接球的直径,求出外接球的直径后,代入外接球的表面积公式,即可求出该三棱柱的外接球的表面积
解答 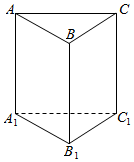 解:由题意,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,
解:由题意,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,
把直三棱柱ABC-A1B1C1补成正四棱柱,
则正四棱柱的体对角线是其外接球的直径,
所以外接球半径为R=$\frac{\sqrt{4+4+16}}{2}$=$\sqrt{6}$,
表面积为S=4π•6=24π.
故答案为:24π.
点评 在求一个几何体的外接球表面积(或体积)时,关键是求出外接球的半径,我们通常有如下办法:①构造三角形,解三角形求出R;②找出几何体上到各顶点距离相等的点,即球心,进而求出R;③将几何体补成一个长方体,其对角线即为球的直径,进而求出R.

练习册系列答案
相关题目
3.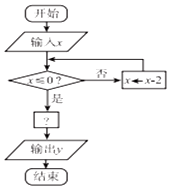 如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )
如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )
 如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )
如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )| A. | y=2x+1 | B. | y=3-x | C. | y=|x| | D. | y=log${\;}_{\frac{1}{3}}$x |
1.在直线2x-3y+5=0上求点P,使P点到A(2,3)的距离为$\sqrt{13}$,则P点坐标是( )
| A. | (5,5) | B. | (-1,1) | C. | (5,5)或(-1,1) | D. | (5,5)或(1,-1) |
2.函数f(x)是定义在R上的偶函数,且在[0,+∞)上是增函数,若f(a)≤f(2),则实数a的取值范围是( )
| A. | (-∞,2] | B. | (0,2] | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |
 如图,五面体ABCDE,四边形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是线段BC上一点,直线BC与平面ABD所成角为30°,CE∥平面ADF.
如图,五面体ABCDE,四边形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是线段BC上一点,直线BC与平面ABD所成角为30°,CE∥平面ADF. 如图1,已知矩形ABCD中,AB=2,$BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.
如图1,已知矩形ABCD中,AB=2,$BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.